二.弹性中子核散射方法简介
1. 前言
前文中我们介绍了中子是如何产生的以及中子源的基本构造,接下来我们讨论如何利用中子和中子的特性来展开针对凝聚态物质的原子结构和动力学的科学研究。我们将首先对中子散射方法的基本原理做一个简单的介绍,即利用中子的穿透性、敏感性和磁性等特殊性质,使其成为凝聚态物理研究领域强有力的微探针,揭示凝聚态物质中原子在哪里、原子如何运动以及磁矩如何排列等诸多关键问题。
当前人们对凝聚态物质的性质和相关物理现象的理解都是建立在原子理论基础之上的。我们在研究任何凝聚态物质体系时提出的第一个问题一定是关于其内部结构的问题,即什么是物质最基本的组成单元以及基本单元是如何排布的。第二个问题往往与物质的微观动力学有关,即这些基本单元是如何运动的,它们运动的自由度又是多少。对于磁性物质来说,我们还希望了解其中由自旋和轨道角动量通过自旋轨道耦合形成的微观磁矩的排列方式,以及它们的磁激发行为。一般来说凝聚态物质的诸多物理特性,例如比热、热导、弹性和磁化率等物理性质都是其微观结构和动力学的外在反映和宏观表现。然而对凝聚态物质科学研究来说,从实验角度确定物质体系的微观结构和动力学是一个巨大的挑战,因为我们面对的是一个包含了1023量级粒子的复杂多体问题。
在微观尺度寻找一个能够有效研究凝聚态物质结构和动力学的探针对于凝聚态物理的发展来说至关重要,而现代散射方法和技术的发展为寻找这类探针提供了坚实的科学基础。X射线作为一种电磁波首先被发现并成为探索凝聚态物质微观结构的无损探针。 德国物理学家劳厄在1912年直接观察到了从单晶散射出的X射线产生的衍射现象,并且提出X射线衍射理论成功解释了衍射现象,因此获得了1914年的诺贝尔物理学奖。这一发现具有非常重要的科学意义,因为这是人类历史上第一个能证明原子是凝聚态物质的基本组成单元,并且以周期性的方式排列在晶体中的确凿证据。自1912年以来,X射线散射方法也得到了飞速发展,时至今日我们对凝聚态物质原子结构的了解绝大多数都是基于X射线晶体结构分析研究的。而随着同步辐射X射线光源的出现,光源的亮度从X射线发现时起发展到现在已经增加了近20个数量级。目前,自由电子激光装置的建设和应用(例如我国在建的位于上海的硬X射线自由电子激光装置)还将使光源亮度进一步提高10个数量级。目前人们已经可以通过同步辐射X射线在原子分辨尺度下确定复杂生物大分子的结构,例如核糖核酸的晶体结构,甚至利用磁性X射线散射方法研究物质的磁性。

中子相较于X射线具有更多特殊的本征性质,这也使其成为与X射线互补的适合凝聚态物质研究的绝佳探针。例如中子衍射特别适用于探知含有氢、锂、碳和氧等轻元素的材料体系的晶体结构,因此可用于研究含有大量轻元素的各种能源材料;中子具有磁性,因此可以应用于磁性纳米颗粒、磁性薄膜和磁性块体材料等多种维度的磁性材料的研究中,一方面可以利用弹性中子散射方法解析磁有序结构、表征磁畴结构、揭示自旋晶格耦合机理,另外还可以利用非弹性中子散射方法研究材料中自旋波激发、晶场激发、磁涨落以及磁阻挫等传统磁性和新奇量子磁性相关问题;中子散射方法可以应用于热电材料的研究中,用于获得声子激发谱,和一些与热导率直接相关的声子特殊的动态行为;在非常规超导材料的研究中,利用非弹性中子散射可以取得超导体中磁激发自旋共振峰等信息并深入理解超导配对对称性等高温超导机理。在软物质和生命科学研究中,中子的优势在于可以通过选择性氘化技术结合中子衍射和准弹性中子散射等方法研究生物大分子的结构及动力学。中子作为微探针几乎可以覆盖凝聚态物质研究中所需的所有空间尺度,从亚原子级的皮米尺度到一个微米的介观尺度。
在此我们首先对弹性中子散射的基本概念中子散射截面进行简单介绍,然后在波恩级数的框架下推导,接着将简单介绍对关联函数,随后我们再讨论中子与物质的相互作用引起的散射长度问题以及三维周期晶格的中子散射,最后简单列举几个弹性中子核散射方法的应用实例。讨论过程中需要注意的是中子作为微观粒子具有波粒二象性,即中子同时具有波和粒子特性,当我们关注干涉现象时,中子在散射过程就可以用波图像进行表述,而当我们关注中子与物质相互作用时,我们就用粒子图像进行表述。
2. 中子散射截面
我们首先假设凝聚态物质中的原子在空间中的平衡位置是刚性且固定的。中子与物质相互作用过程中的反冲作用被完全转移到样品中,也就是说中子在相互作用过程中的能量变化可以忽略,这样的散射过程我们就可以认为是弹性中子散射过程。如果我们取消前述的这个限制那么就会引入和考虑所谓的非弹性中子散射过程。非弹性中子散射过程的发生一定伴随着中子能量的变化,而这种能量的变化往往是由凝聚态物质中的激发或涨落对中子的散射而引起的,因此中子能量的变化也和物质中的特征能量相关。我们在这里先讨论弹性中子散射方法,今后再对非弹性中子散射方法进行讨论。图1所示为中子散射实验的示意图。

图1 在夫琅和费近似下的中子散射过程示意图。
这里我们首先需要对散射过程做一个夫琅和费近似,即样品物质的大小远远小于样品与中子源之间的距离以及样品与探测器之间的距离。此外,我们假定中子源发出的是确定能量的中子,即所谓的单色中子。那么我们可以把入射到样品物质上的波场看作是一个平面波,它可以用一个波矢量k来表示,同样入射到探测器上的波也可以用一个波矢量 k‘来表示。在弹性中子散射的限定条件下我们可以得到:

我们把散射矢量定义为:
![]()
ħQ代表在中子散射过程中发生的动量转移,波矢为k的波对应的粒子的动量可以用公式p =ħk确定。散射矢量的大小可以用波长λ和散射角2θ计算得到:
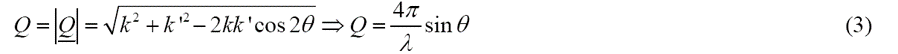
对于弹性中子散射实验来说,测量的核心内容是中子散射强度分布随散射矢量Q的变化,即散射矢量的函数I(Q)。散射强度正比于中子散射截面,定义中子散射截面的示意图见图2。

图2 定义中子散射截面的几何示意图。
假设在2θ的散射角下,每秒钟有n’个中子被散射并进入探测器的探测立体角dΩ ,同时中子的能量还能够落在E’ 至E’ + dE’ 之间的能量范围,那么我们就可以通过下面公式来定义双微分截面:

在此公式中j是入射中子束流的通量,可以用单位时间内通过单位面积的中子个数来表示。如果我们对散射过程中的能量变化不感兴趣,那么我们可以直接用微分截面来表示散射过程中的角度依赖性:

这样我们也能得到总散射截面,总散射截面与总散射概率有关但与能量和散射角的变化都无关。

接下来我们的任务就变成了根据散射截面dσ/dΩ来确定样品物质中原子的排布情况。在波恩近似条件下,发生在样品物质内的入射束和出射束的折射问题、多次散射现象以及初级束流的消光等都可以忽略,因此散射强度与样品物质结构之间的关系非常简单。在这种近似条件下,坐标系原点和位置r处的两点A和D之间的相位差(图3)可以表示为:

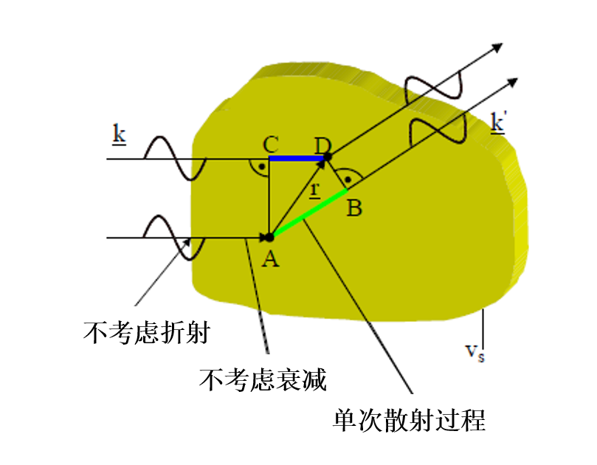
图3 坐标原点处A点与位置r处D点的散射中子束的相位差示意图。
位置r处的散射振幅与该位置的散射密度ρs(r) 成正比,ρs(r)取决于中子束流与样品物质之间的相互作用。在这里ρs(r)直接与相互作用势能成正比。我们假设有一个横向相干中子束流射入,那么总散射振幅由样品中所有点的相干散射叠加得到:

其中A0表示入射波场的振幅,同时式8还表明散射振幅可以通过简单的傅里叶变换与散射密度相关联。因此只要我们知道了所有散射矢量Q的散射振幅,那么我们就能够通过傅里叶变换得到唯一确定的散射密度,散射密度就包含我们希望通过中子散射实验得到的样品物质的微结构信息。但是实际操作起来也并没有这么简单,一方面,确定对应于所有动量转移ħQ值的散射截面存在很大的技术难度,另一方面根本问题在于我们只能测量散射强度而无法测量散射波的振幅。
![]()
相位信息的缺失使我们不能通过简单的傅里叶变换来重建散射密度,这也就是经常被提及的散射方法结构解析的相位问题。在X射线法解析复杂结构过程中相位问题也是核心问题。虽然中子散射存在相位问题,但是我们还是可以从中子散射实验中获得很多关键信息,下面我们进一步探讨。除此之外,在弹性中子散射实验中选择合适的中子波长也是得到所需实空间分辨率的关键。如果想得到长度尺度为L的物质的结构信息,那么就必须具备大约Q⋅L ≈ 2 π的相位差,否则根据式7,k’ 与 k就不会有显著差别。同时还要考虑Q ≈ 2π / λ 所对应的典型的散射角 (一般2θ = 10 ~ 140°)。结合考虑这几方面因素,我们就能得出适用于研究对象的实空间长度的波长λ值。例如在中子波长为1 Å的前提下,中子散射实验可以具有原子尺度的空间分辨率。
3. 波恩级数
在量子力学框架下我们用薛定谔方程描述中子在势场中的波函数:

其中ψ为概率密度振幅,V是相互作用势场。在弹性散射E = E’ 的情况下,时间依赖性可以用指数因子来表示。概率密度振幅的空间部分的波动方程可以从式10推导得到:
![]()
在上式中,我们引入了一个空间变化的波矢,该波矢的模平方为:

式10的真空解,即V ≡ 0 的解可以很容易得出。即,其中。因此波矢k的振幅,波长λ以及中子的能量E之间的关系可以写成:

例如,波长λ = 2.4 Å 的中子的能量为14.2 meV,波矢的大小为k = 2.6 Å-1。
为了获得中子在物质中波动方程的解,我们通过分离相互作用项来重构微分方程:

其中k为真空中传播的波矢。 这个公式的等号左侧有已知解,就是真空中的平面波。 式(14)是一个线性偏微分方程,因此满足线性微分方程的叠加原理,可以得到一组完整函数的线性组合通解。 应用非齐次线性微分方程求解法对式(14)求解,我们首先假设等号右边是固定值(给定为χ),然后定义一个格林函数如下式:
![]()
上式的解为:

这个等式表明点状散射体的散射是一个散射球面波,如下图所示:
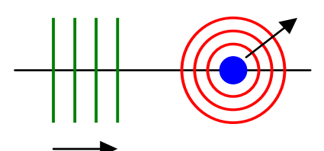
通过格林函数G(r,r’),我们可以将波函数的形式解写为:
![]()
把(17)代入(14)可以发现(17)其实就是式(14)的解。如果我们最后代入函数,就能得到李普曼-施温格方程:
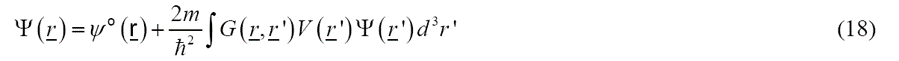
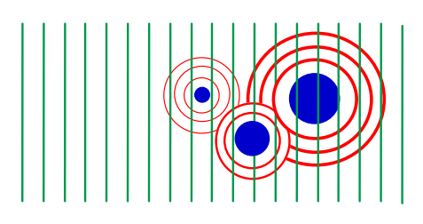
式(18)可以简单地理解为:入射平面波Ψ0(r)与位置r’处散射发出的球面波叠加,而这些球面波的强度正比于r处的相互作用势V(r’)及波场的振幅。我们对整个样品物质的体积Vs进行积分就可以得到总散射振幅。
可以看到在式(18)中又出现了Ψ,也就是说我们仍然还没有完成式(14)的求解,我们只是把微分方程(14)转变成了积分方程,而积分方程的优势在于可以通过迭代就找到一个解。在零阶近似的条件下我们可以忽略相互作用V,即Ψ = Ψ0。通过代入式(18),可以得到弱相互作用势下的一阶近似,这也是描述波传播的惠更斯原理的数学表述:
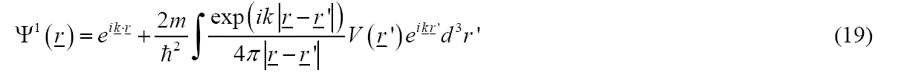
上式假定入射平面波只被势能V(r’)散射一次, 但是对于大尺寸样品和强势,也会发生多重散射的过程,这个过程也可以通过进一步的迭代从积分方程(18)中推导出来。
为了简化方程我们引入方程(18)的一个新形式,即把格林函数的积分写成算符G:
![]()
把等式右边的波函数ψ替换为ψ0,即可得到描述运动散射理论的一阶波恩近似 :
![]()
这个一阶近似可以用简单的示意图表示为入射平面波和势V处散射一次的波的总和:
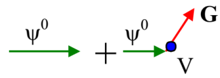
将(21)代入(20)可以得到二阶近似,即:
![]()
也可以用简单的示意图表示为:

在二阶近似中还考虑了中子被相互作用势V二次散射的过程。采用这样的方法可以计算得到所有高阶近似,这也就是所谓的波恩级数。对于弱势和小样品来说波恩级数会很快收敛,因此通常基于一阶近似的运动散射理论就可以很好的描述中子散射过程。然而对于X射线和电子散射来说,因为存在强库伦相互作用势,所以X射线和电子在物质中发生多重散射的几率很高,进而增加衍射实验数据分析的难度。实际上即使对于中子散射来说,运动散射理论也不是完全百分之百适用,比如在研究理想大单晶的布拉格中子衍射过程中,波恩级数可能不收敛,波动方程必须在晶体几何给出的边界条件下才能精确求解。
回到一阶玻恩近似(19),在进一步的夫琅和费近似中,我们假设样品的尺寸远小于样品和检测器之间的距离,计算远场极限的几何结构如图4所示。假设,我们可以推导出散射球面波的以下近似关系:
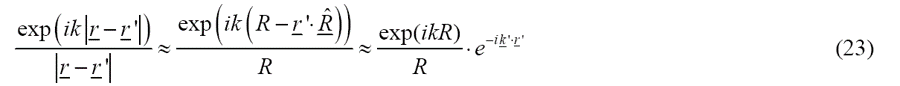
在距离样品大于极限距离的条件约束下,散射波场的几率密度振幅由下式给出:
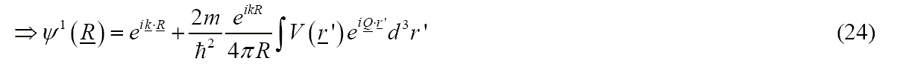
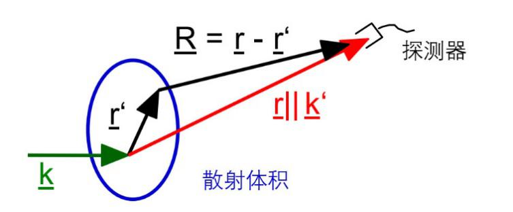
图4 用于计算探测器远场极限的散射几何,在夫琅和费近似下假设。
这就是入射平面波和整个样品的散射球面波的总和。散射波的振幅由(25)给出:

上式中积分部分是初始和最终平面波状态之间相互作用势V的转换矩阵元,因此有:

这个公式对应于含时微扰理论中的费米黄金法则,其中从状态k到状态k’的每个时间间隔的转换概率为:

其中代表终态k’的态密度。通过与式(8)比对 可以发现受薛定谔方程支配的粒子束的散射密度为:
![]()
如果我们考虑非弹性中子散射过程,那么样品物质还会经历一个从α到α’的状态变化(α是表示样品本征态的一组量子数)。因为入射波和出射波的波矢不同,所以我们必须引入与态密度关联的因子k’和k。中子散射过程必须满足能量和动量守恒,因此我们可以得到双微分截面:
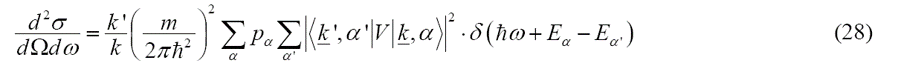
第一个求和项是对材料体系中所有可能的初始状态α以及它们的热力学占据概率pα权重进行加权求和。对α’的求和是能量守恒条件下符合δ-函数的所有最终状态的和。表示从中子到体系的能量转移。关于这个双微分截面我们将会在今后的非弹性中子散射方法简介部分做进一步讨论。
4.对关联函数
在讨论了中子散射的波恩近似之后,现在我们回到从中子散射实验中获得散射强度之后如何获得结构信息的问题。从式(9)中,我们已经知道在测量中子散射强度的过程中并不能得到相位的信息。把式(8)带入(9),同时令R=r‘–r,我们就可得到振幅模的平方的表达式,它可以通过中子散射实验直接获得:
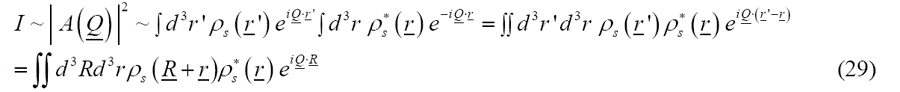
上式表明,散射强度与函数P(R)的傅里叶变换成正比:
![]()
这个方程定义了晶体学中的帕特森函数,也就是静态对关联函数:
![]()
帕特森方程P(R)把位置为r和r+R的散射密度数值关联起来,然后再对整个样品体积进行积分。如果样品在r和r+R处的散射密度值彼此不相关的话,那么P(R)就会消失。如果样品中位置差为R的原子对周期性排列,那么帕特森函数就会在R处出现一个极值。因此,帕特森函数重现了所有周期结构中连接一个原子和另一个原子的矢量。
我们通过中子散射实验就可以确定对关联函数。在非弹性相干中子散射实验中,我们可以测得S(Q,ω),即空间-时间对关联函数的傅里叶变换:

其中比例因子由所研究材料体系和中子的相互作用势决定。时间-空间对关联函数为所研究材料体系本身的性质:
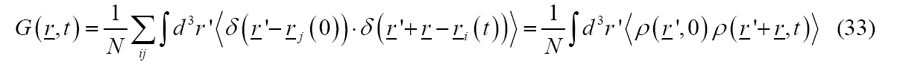
对关联函数可以表示为N个点状粒子位置之间的关联关系,也可以表示成样品物质内不同位置不同时间的密度间的关联关系。对于磁性材料体系,通过中子散射实验我们可以观察到磁散射信号,对应于自旋对关联函数的傅里叶变换。
5. 三维周期晶格的中子散射
如果想得到中子散射截面那么就必须首先得到中子与原子核的相互作用势。由于中子散射实验中中子的波长远大于原子核半径,因此我们可以把原子核看做是能够引起各向同性散射的很小的散射点。基于这个事实费米提出了一种唯象势来估算散射截面,即费米赝势:

虽然原子核对中子的散射过程由强相互作用主导,但是由于原子核尺寸小因此散射概率也很小,我们依然可以采用一阶玻恩近似来处理。式中b是描述相互作用势强度的值,也就是中子散射长度。不同元素的中子散射长度b值可以在参考文献或中子科学研究机构的网站上查到。原子核的总散射截面为对应于半径为b的球体的表面积。另外相互作用势与复杂的原子核结构密切相关,所以不但对于不同的元素,就算是对于相同元素的不同同位素甚至是不同的核自旋态,中子散射长度b也不同。图5展示了整个元素周期表中不同元素的中子散射长度随原子量的变化情况,X射线散射长度也画在图中做对比。可以看到大多数元素的中子散射长度都为正值,但有一些元素的散射长度为负值。由于-1 = exp(iπ),所以这里中子散射长度的负号对应于散射过程中的180°相移。和X射线散射长度不同,不同元素的中子散射长度并不随原子序数连续变化。

图5 元素周期表中中子和X射线散射长度与原子序数的关系。
绝大多数凝聚态物质都具有三维周期晶格结构,我们下面讨论中子在三维晶格中的散射情况。首先我们给定一个简单的具有布拉格晶格结构的单晶,并且单位晶胞中只有一个原子,每个原子的散射能力设为α。单晶在沿基矢、、分别具有N、M、P个有限周期。式(8)中的散射密度是所有散射中心的δ函数之和:
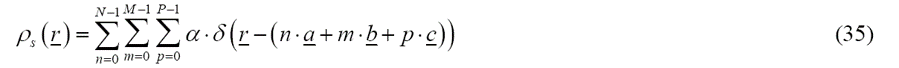
通过傅里叶变换计算散射振幅:

对几何级数求和,得到散射强度:
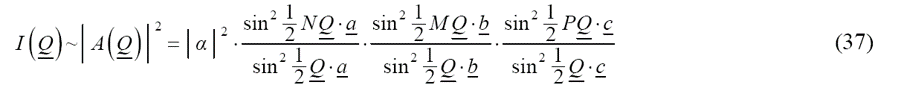
通过对劳厄方程在三维空间方向上进行因式分解得到散射强度与散射矢量Q之间的关系。沿晶格方向的一个因式如图6所示。
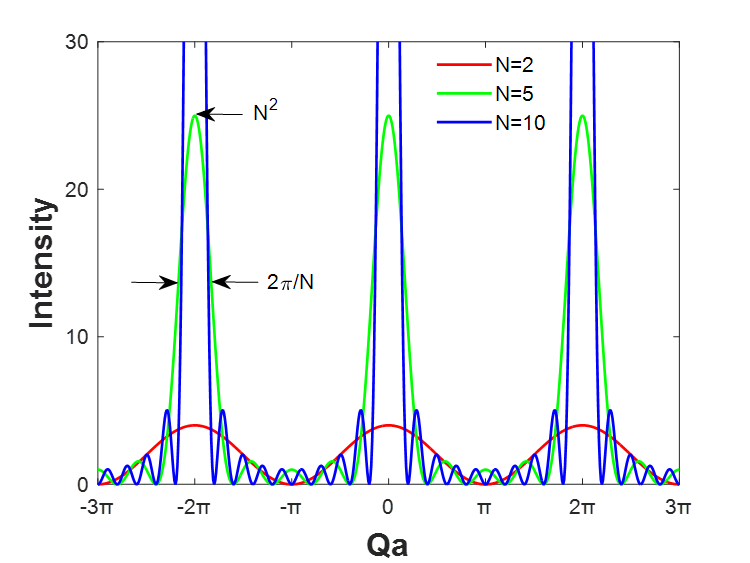
图6 分别具有2、5、10个周期的沿晶格方向的劳厄函数。
从上图可以看到强度最大值出现在Q = n·2π/a处。最高峰强度随周期数平方N2变化,半峰宽约为ΔQ = 2π/(n·π)。相干散射的周期数越多,主峰就变得越强越尖锐。另外,主峰之间还存在有N-2个副峰,随着周期数N的增加,它们的强度相较于主峰强度会变的很弱甚至可以忽略不计。这里的主峰就对应于从晶格中子散射中直接得到的布拉格衍射峰。我们通过布拉格衍射峰在动量空间中的位置就可以推算出晶体材料的晶胞参数(晶格参数a、b、c和晶格角度α、β、γ)。布拉格衍射峰的峰宽由相干散射体积和实际中子散射实验中的仪器分辨率和材料内部应力等一些其他因素共同决定。
6.弹性中子散射方法应用实例
弹性中子散射方法包括弹性中子核散射和弹性中子磁散射,分别对应于晶体结构的确定和磁结构的解析。根据样品物质不同的形态和实验的需要还可以选择粉末中子衍射和单晶中子衍射方法等不同的衍射方法。这里我们先展示几个弹性中子核散射方法的应用实例。如前言所述,中子散射非常适合于研究含有锂和氧等氢元素的材料体系,例如我们在日常生产生活中应用非常广泛的锂离子电池材料,这里我们以锂离子电池正极材料结构的中子衍射研究为方向展开举例。
锂离子电池作为新一代电池具有重量轻、比能量高、使用寿命长等特点,被广泛应用于电子产品、军用产品和航空产品。在所有的锂离子电池正极材料中,含有过渡金属镍、锰和钴的三元层状氧化物材料是非常具有应用前景的正极材料。然而,该类材料中普遍存在影响材料充放电性能的锂镍反位结构缺陷。X射线衍射等常规实验方法难以对这种微量结构缺陷进行精确确定。我们知道X射线的散射截面大小取决于原子核外电子的数量,因此散射截面在整个元素周期表中以单调增加的方式变化。在样品物质中存在金属离子等重元素的情况下用X射线就很难确定锂的位置。此外,从图5中也可以看出对于X射线来说,过渡金属镍、锰和钴相邻元素之间的散射截面差别非常小,因此难以对这三种金属元素进行有效区分。而中子的散射截面取决于核结构,对样品材料中各个元素都有很高的对比衬度。
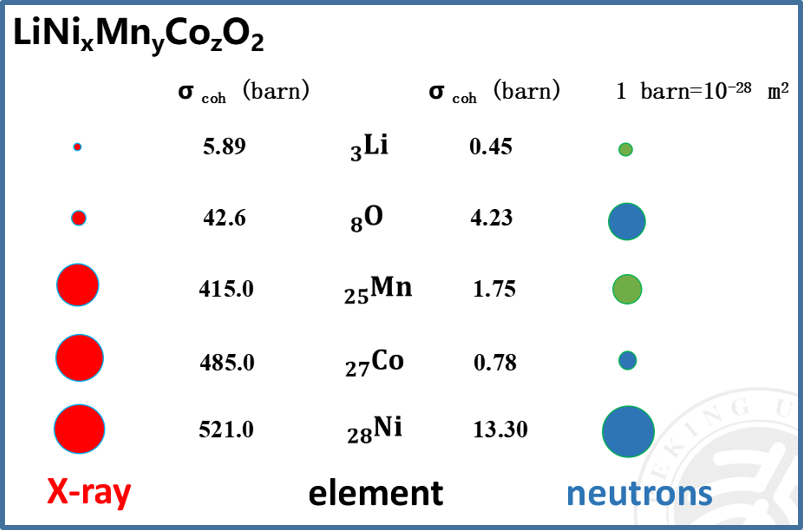
图7 层状氧化物正极材料中几种元素的X射线和中子相干散射截面的比较。彩色圆形的面积表示散射截面大小,X射线的散射截面比例因子为10。中子散射截面中蓝色和绿色圆形分别代表具有正和负的散射长度。
利用中子对锂原子和镍锰钴过渡金属原子均非常敏感的这一特性,我们采用中子衍射方法,在中国散裂中子源(CSNS)的通用中子粉末衍射仪(GPPD)和美国国家标准与技术研究院(NIST)的BT1中子衍射仪上对一系列锂离子电池三元层状正极材料的晶体结构进行了精确的表征。通用中子粉末衍射仪GPPD为依托脉冲式散裂中子源的谱仪,因此采用飞行时间中子衍射方法,这是一种固定角度的波散技术。通过测量中子被样品材料散射之后到达探测器位置的时间就能够得到中子的飞行速度和波长,这样就可以充分利用宽波段的白光中子,在特定的散射角得到材料在Q空间的散射信号分布信息。而BT1中子衍射仪为依托反应堆中子源的谱仪,因此采用固定波长中子衍射方法,是一种单波长变角度的技术。通过测量中子被样品材料散射后的角度和强度分布获得在Q空间的散射信号分布信息。虽然这两种方法原理上略有差异,并且存在各自的优缺点,但是最终得到的数据中包含的信息是一致的。

图8 (a) 锂离子电池层状正极材料的晶体结构,(b-d) 不同组分正极材料的高分辨中子粉末衍射谱,(e)层状材料中不同组分与锂镍反位量之间的关系。
基于对锂离子电池三元层状正极材料的中子衍射实验结果,我们建立了三元材料体系中反位缺陷随过渡金属组分的变化规律,提出了材料中锂镍反位与三角晶格阻挫结构特征之间存在关联关系的观点,并从这一新颖的角度对锂镍反位缺陷结构的形成做了自洽的解释。这些重要结果有助于进一步澄清材料中缺陷结构与电池材料性能之间的关系,并且在对三元锂离子电池正极材料的开发过程中起到直接的指导作用,文中的观点也被《科学》杂志的展望文章引用评述。位于广东东莞的中国散裂中子源(CSNS)是我国“十一五”国家重大科技基础设施,也是我国第一个脉冲式中子源。中国散裂中子源于2017年8月首次打靶成功并获得中子束流,11月达到打靶束流功率的验收指标,并于2018年3月通过了工艺鉴定和验收。上述锂离子电池正极材料结构的中子衍射研究工作依托散裂源的通用粉末中子衍射谱仪完成,是中国散裂中子源建成以来的首篇科学研究文章。

图9 位于中国散裂中子源散射大厅的通用粉末中子衍射谱仪(GPPD)。
除了中国散裂中子源以外,我国还有位于北京的中国原子能研究院先进研究堆CARR中子源,以及位于四川绵阳的中国工程物理研究院绵阳研究堆(CMRR)中子源。我们在这两个反应堆中子源的中子衍射谱仪上也顺利完成了一系列中子散射研究工作,可以说依托两个反应堆中子源的几台中子衍射谱仪都表现不俗,能够满足不同类型材料的结构分析需求,并取得创新性成果。在中子科学的前辈和同仁的共同努力下,我国的这些先进中子源得以高效运行,并快速推动了我国中子散射科学的发展和应用。
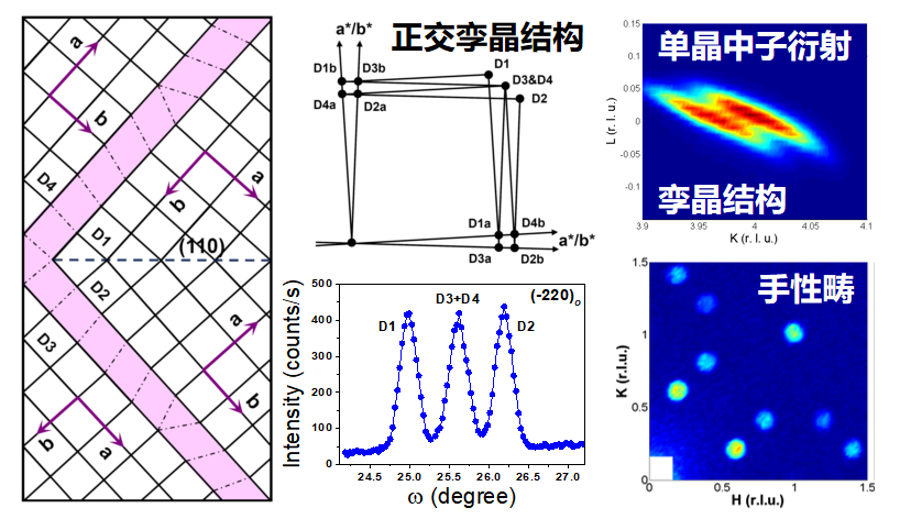
图10 实空间中的孪晶结构和通过中子单晶衍射方法得到的孪晶结构倒空间中子衍射斑点。
总之,中子散射方法能够在解决凝聚态物质结构问题的研究中发挥巨大优势,但是在设计实验时首先需要对中子的能量、波长和散射矢量范围等方面做全面的考量。此外还要根据样品物质的形态选择适当的中子散射谱仪,中子粉末衍射谱仪快速高效可以解决大多数粉末状材料的结构问题,而采用中子单晶衍射谱仪可以得到晶体材料中具有各向异性特点的微结构,例如图10中所示的孪晶结构和手性畴结构。采用中子全散射谱仪不但可以获取样品的长程有序布拉格衍射峰,而且还可以得到材料中伴随短程或局域原子有序产生的漫散射信号,结合原子对分布函数分析方法可以深入表征短程和局域有序结构。图11是中子、电子和光子这三种微探针的波长-能量对应关系图。可以看到25 meV的中子就可以很好的探测埃米尺度的原子间距,而对于纳米尺度的材料就需要中子小角散射来研究。在应用中子散射方法之前还需要考虑样品材料中是否含有强中子吸收元素以及是否有较强的非相干散射背景,只有做好实验设计才能保证实验的顺利进行并能够取得包含丰富结构信息的散射信号。另外需要注意的是中子的散射截面一般比X射线的散射截面小大约10倍,也就是说在相同的束流通量和样品尺寸条件下,中子散射的信号要比X射线弱很多,因此对于中子散射来说需要更大量的样品。
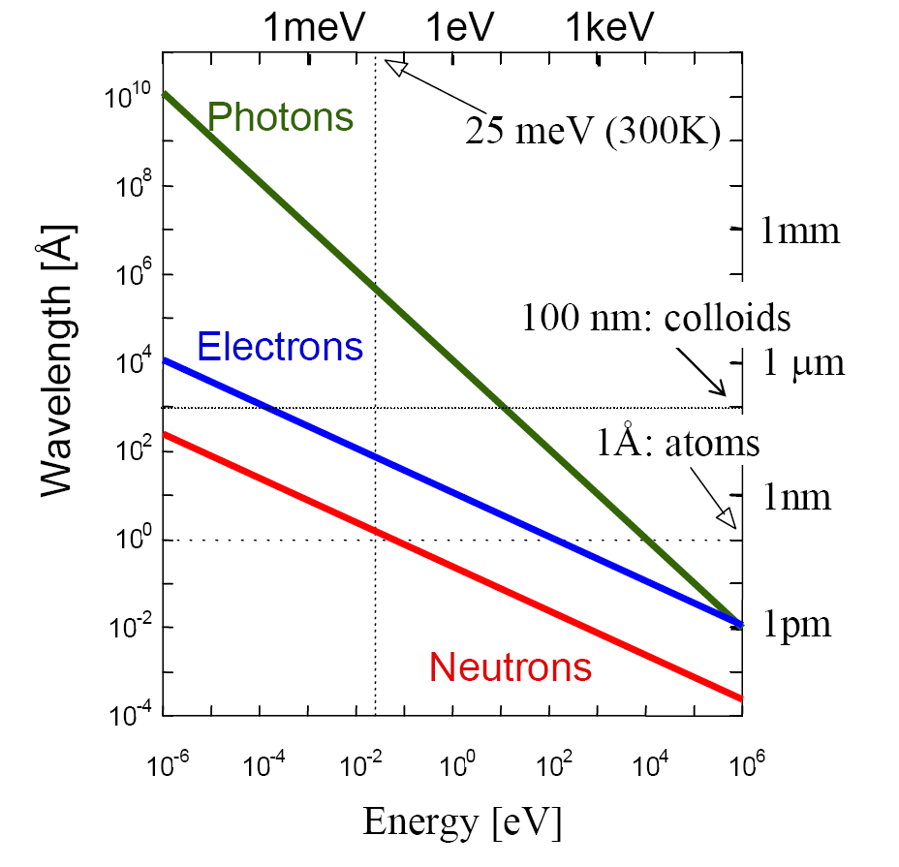
图10 中子、电子和光子三种探针的波长-能量对应关系图。
参考文献
[1] S. W. Lovesey, Theory of neutron scattering from condensed matter (1987) Clarendon Press, Oxford.
[2] K. Sköld, D. Price (Eds.), Methods of Experimental Physics (1987) Academic Press, London.
[3] G. L. Squires, Introduction to the Theory of Thermal Neutron Scattering (2012) Cambridge University Press, New York.
[4] A. Furrer, J. Mesot, T. Strässle, Neutron Scattering in Condensed Matter Physics (2009) World Scientific, London,
[5] Th. Brückel et al., Neutron Scattering (2008), Forschungszentrum Jülich, Jülich.
[6] H. Chen, X. Wang, Nat. Mater. 15, 689 (2016).
[7] J. Chen et al. Phys. B Condens. Matter 551, 370–372 (2018).
[8] Y. Xiao et al., Nano Energy 49, 77-85 (2018).
[9] Y. Xiao, et al., Phys. Rev. B 80, 174424 (2009).
[10] 程贺,张玮,王芳卫,陈延伟. 中国散裂中子源的多学科应用[J]. 物理, 2019, 48(11): 701-707.
[11] 郭尔佳,朱涛. 中子散射在磁性材料研究中的应用[J]. 物理, 2019, 48(11): 708-714.
[12] 王国华,焦金龙,马杰. 中子散射技术在功能性材料中的应用[J]. 物理, 2019, 48(11): 715-725.
[13] 韩晶晶,储祥蔷. 利用中子散射探索生命世界中的物理奥秘[J]. 物理, 2019, 48(12): 780-789.
[14] 沃弘樑,王奇思,沈瑶,赵俊. 非常规超导体的中子散射研究[J]. 物理, 2019, 48(12): 790-799.
[15] 盛洁明,童欣,吴留锁. 非弹性中子散射在稀土钙钛矿研究中的应用[J]. 物理, 2019, 48(12): 800-807.