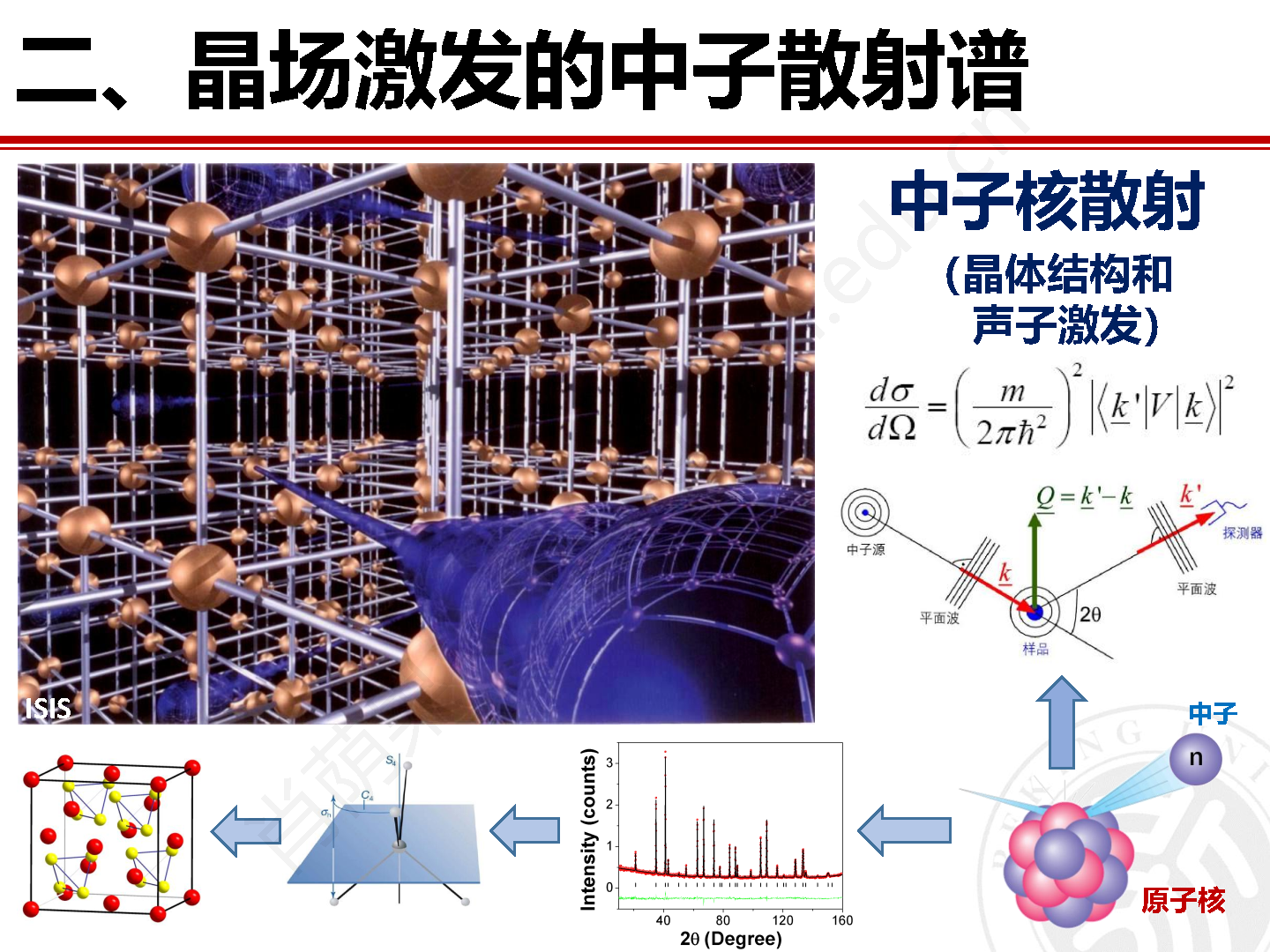
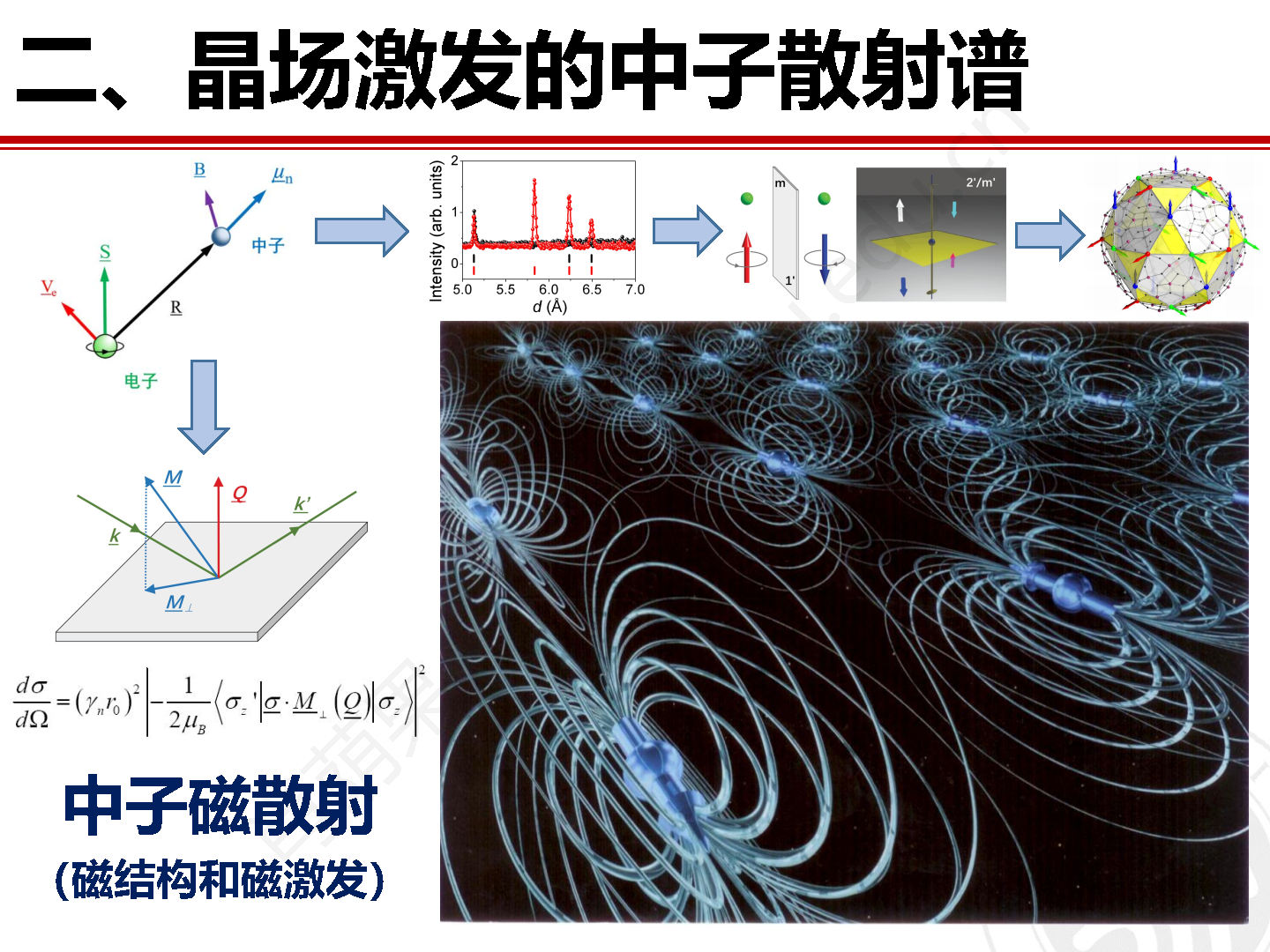
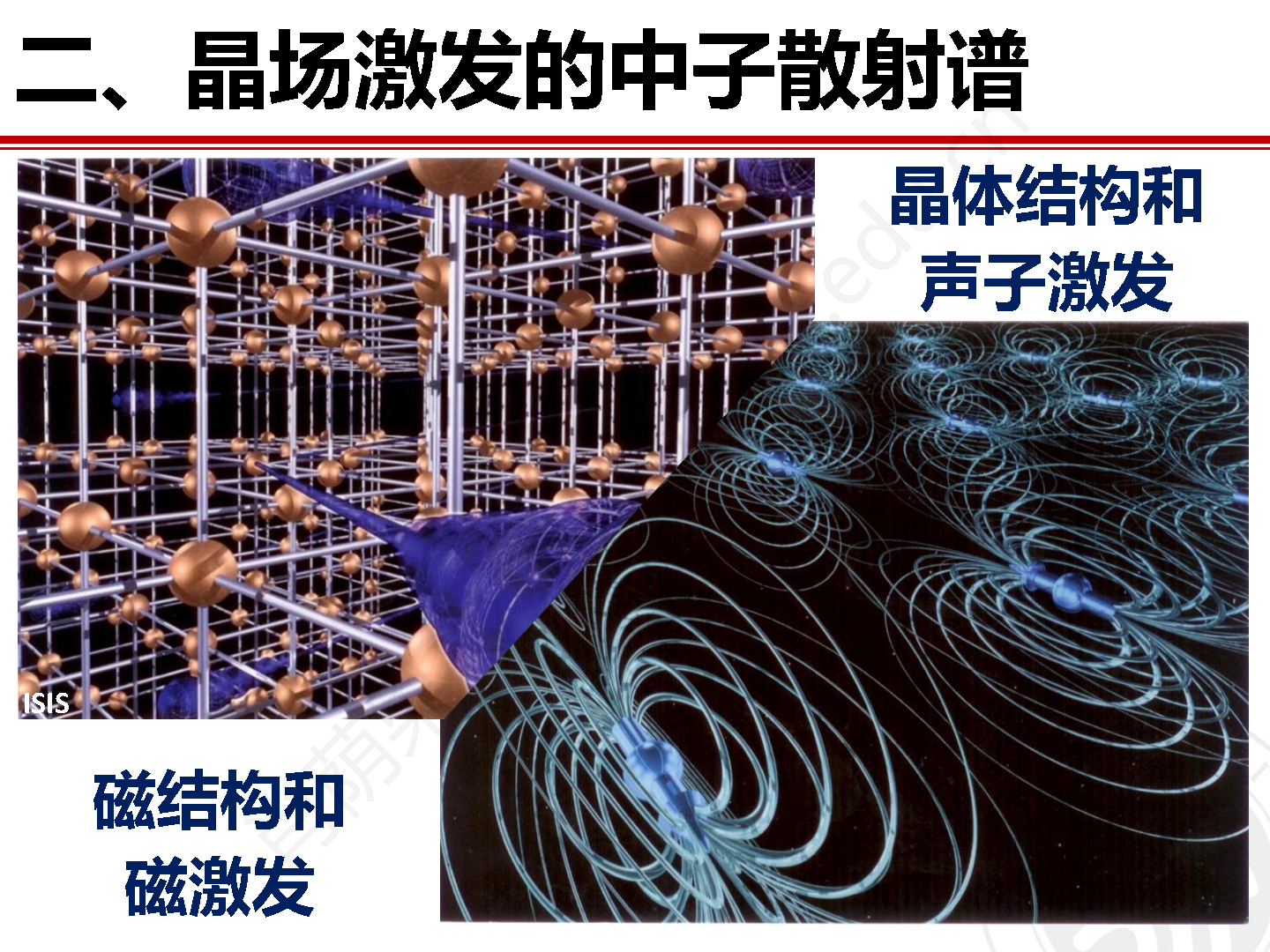
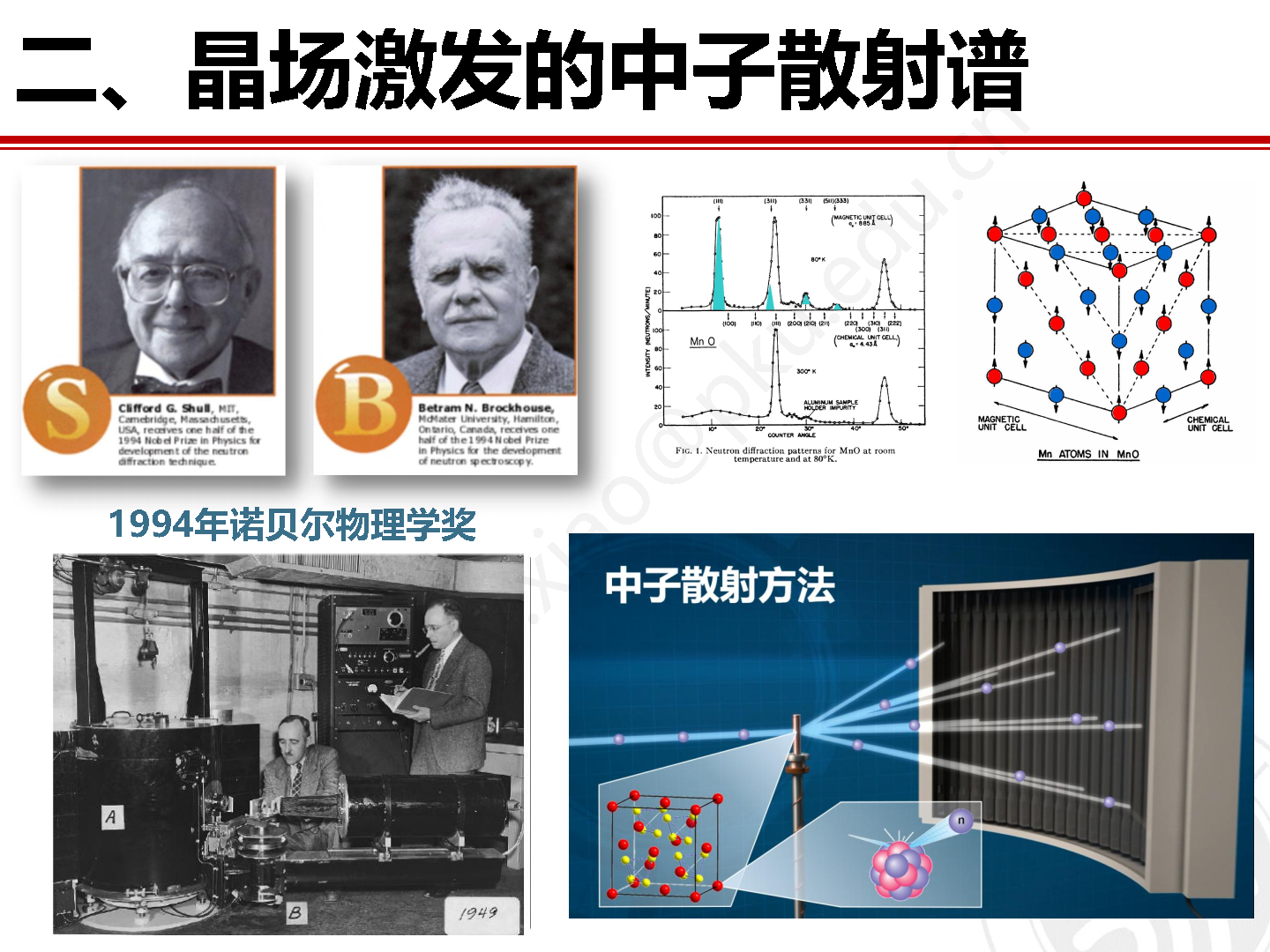
五、非弹性中子散射方法之晶场激发
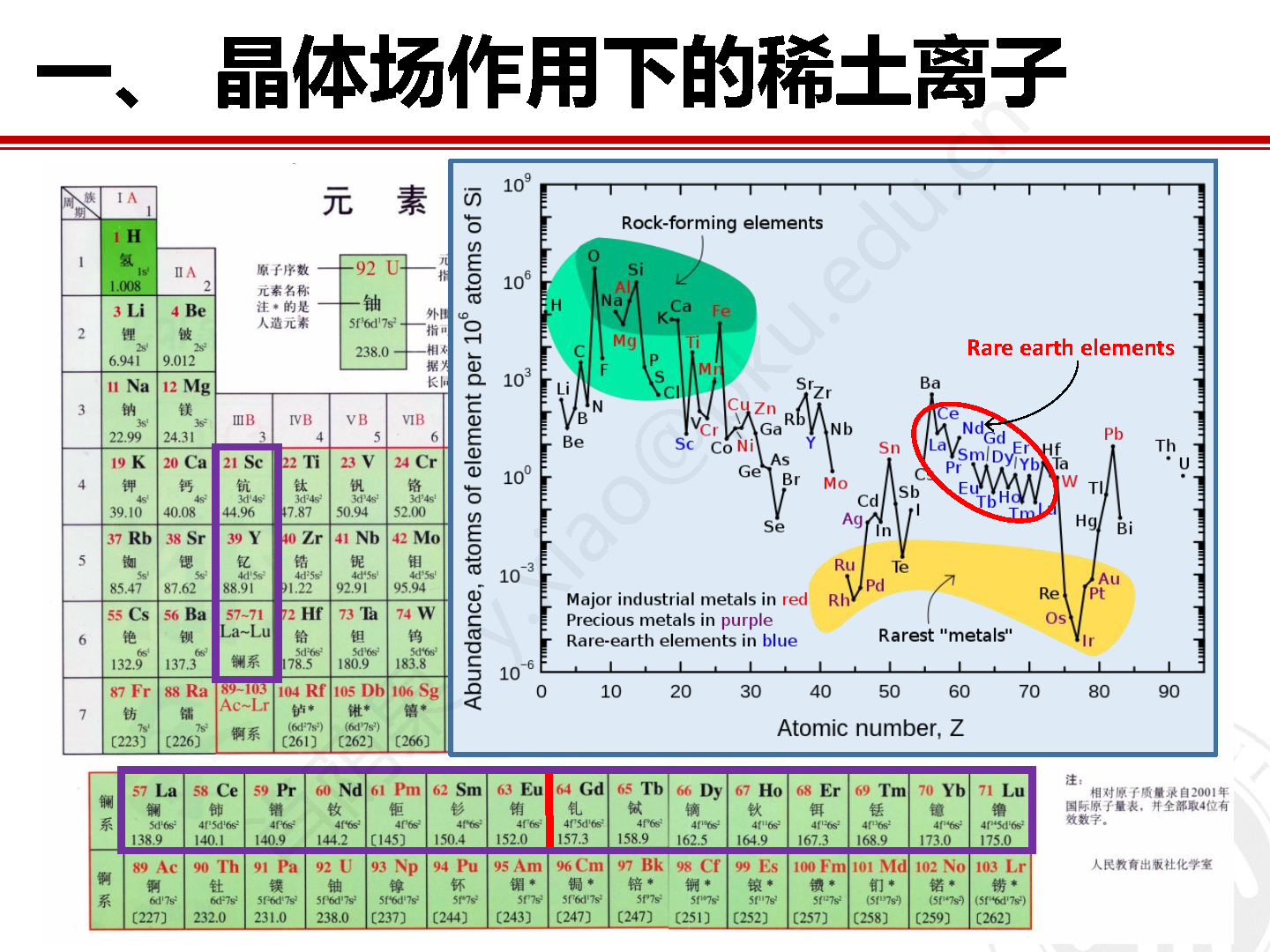
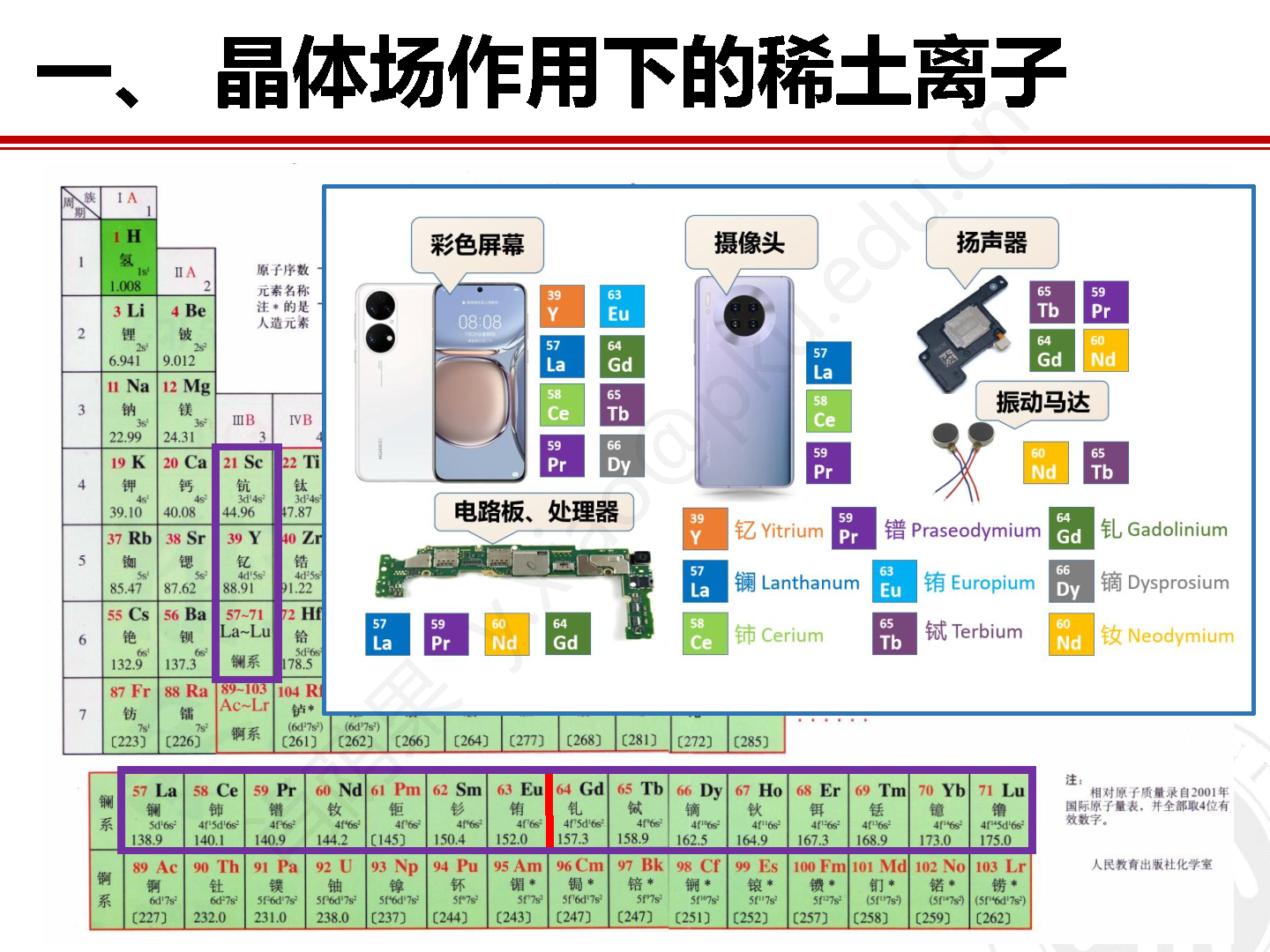
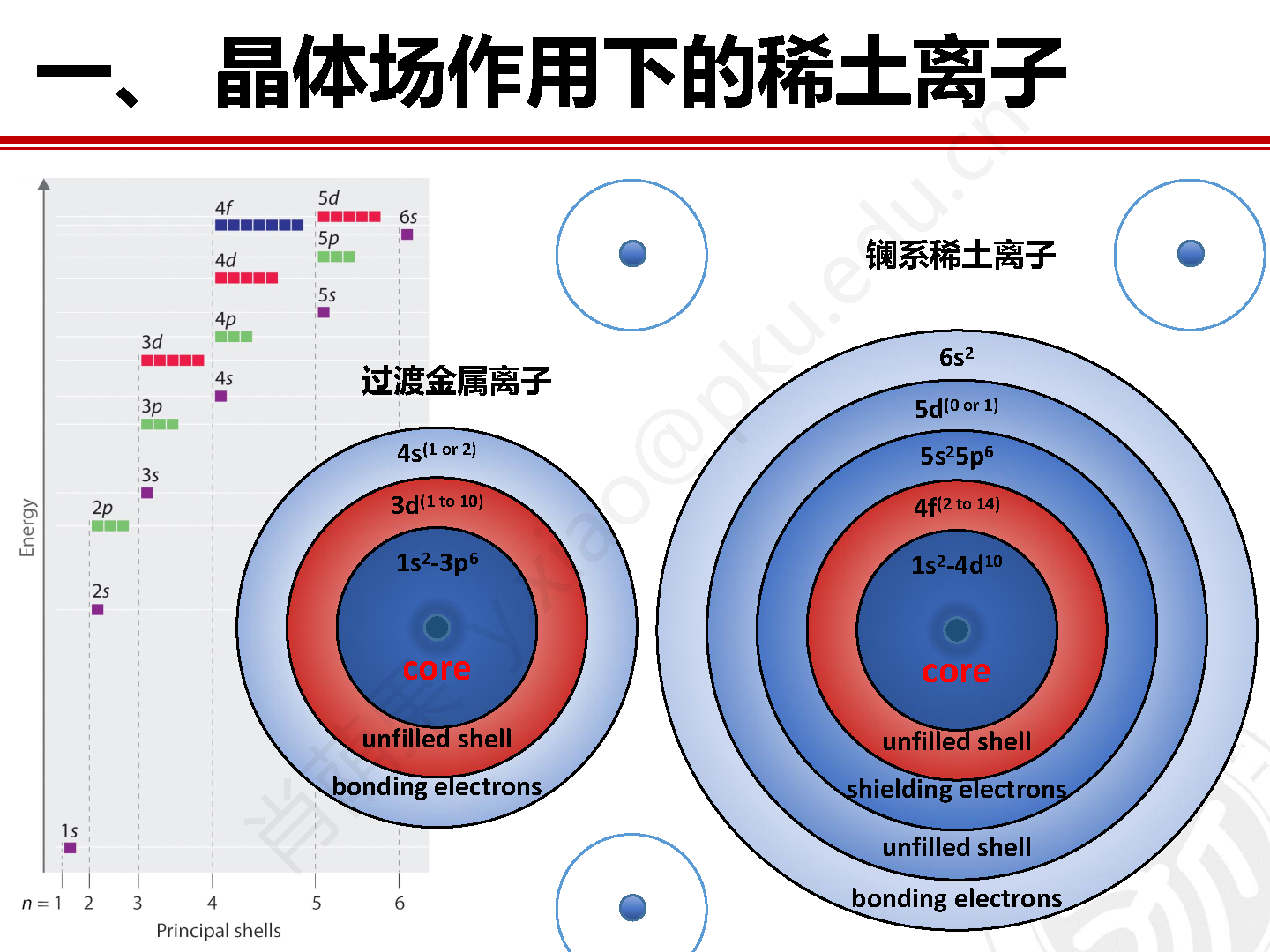
晶体中过渡金属或稀土磁性离子上的电子会受到周围配位离子的静电场作用力,导致简并的电子轨道能级发生劈裂并形成具有不同能量的单态或多重态。对于稀土元素来说,其4f电子密度主要集中在原子内层,因此外层电子能够起到屏蔽晶场的作用,这也使得晶场作用于4f电子的能量要远小于其自旋轨道耦合能。稀土离子的晶场能量一般在一百毫电子伏特以内,而这一能量范围恰好和非弹性中子散射方法的能量探测范围匹配,因此非弹性中子散射方法是表征稀土材料中不连续晶场劈裂能级和晶场激发的重要独特方法。在晶场理论的框架下,通过对晶场哈密顿量的解析可以对非弹性中子散射实验数据进行拟合,并取得重要的能够反映稀土化合物的比热、磁化率、磁熵、电阻和热膨胀等一些列重要宏观物性的稀土晶场结构信息。
1. 晶场理论简介
晶场理论是一种能够简单有效描述配位化合物中围绕某中心位点形成三维离域性配位键的方法。晶态体系中中心原子的d或f电子在实空间中通常会展现出和s或p轨道不同的具有取向性的轨道结构,因此所形成的配位键会表现出一定的离域性。晶场理论能够结合静电理论和体系的量子特性对晶体中的配位键和电子轨道劈裂的形成机理进行自恰的解释,并能够揭示体系热力学、磁学和电学等诸多物理性质的形成机理。
晶格中磁性原子的哈密顿量可以表述为:
![]()
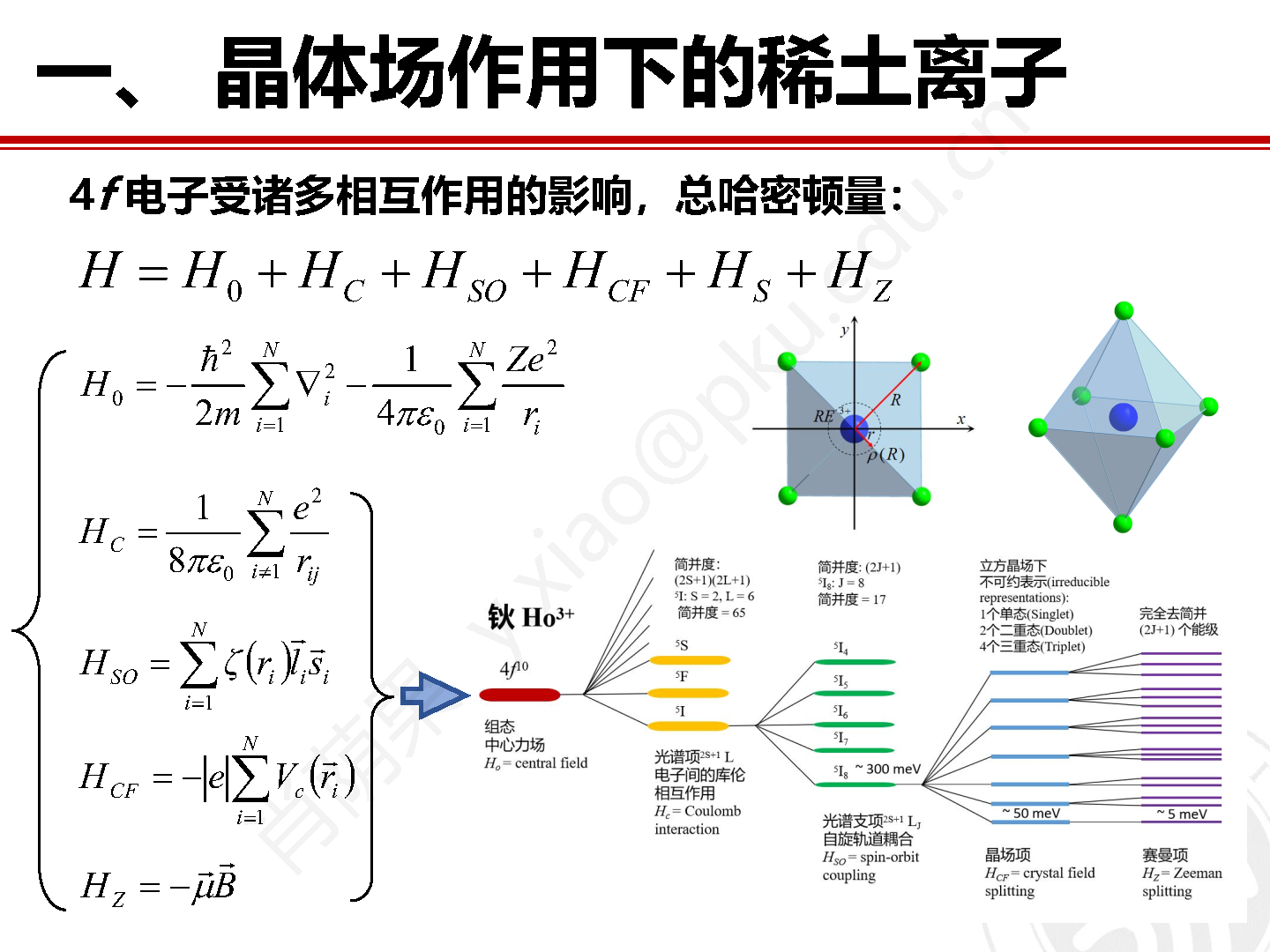
其中 H0 包括中心原子中电子的动能以及电子和电子之间的库伦相互作用。HSO 代表自旋轨道相互作用。HCF 为晶场作用项。HS 为磁交换相互作用。HZ 为塞曼相互作用项。总哈密顿量中不同相互作用的能量值大小也不尽相同。
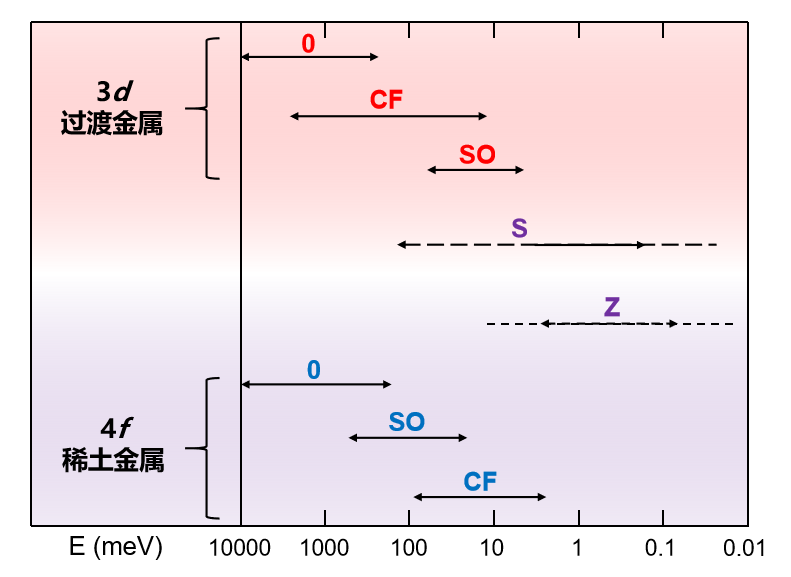
图1 3d 过渡金属和 4f 稀土体系中电子受到不同类型相互作用影响的能量相对关系。
如图1所示,H0 项能量最大,HZ 项能量贡献最小。对于 3d 过渡金属来说,其 3d 电子轨道暴露在外,晶场作用能量远大于自旋轨道耦合能 ( HCF > HSO ),因此 3d 电子轨道能级在晶场作用下劈裂并伴随轨道角动量的淬灭。而对于稀土元素来说,一方面 4f 电子密度主要集中在原子内层,外层电子能够起到屏蔽晶场的作用,另一方面自旋轨道相互作用正比于电子数量,因此一般来说其自旋轨道耦合能远大于晶场作用能量 ( HSO > HCF )
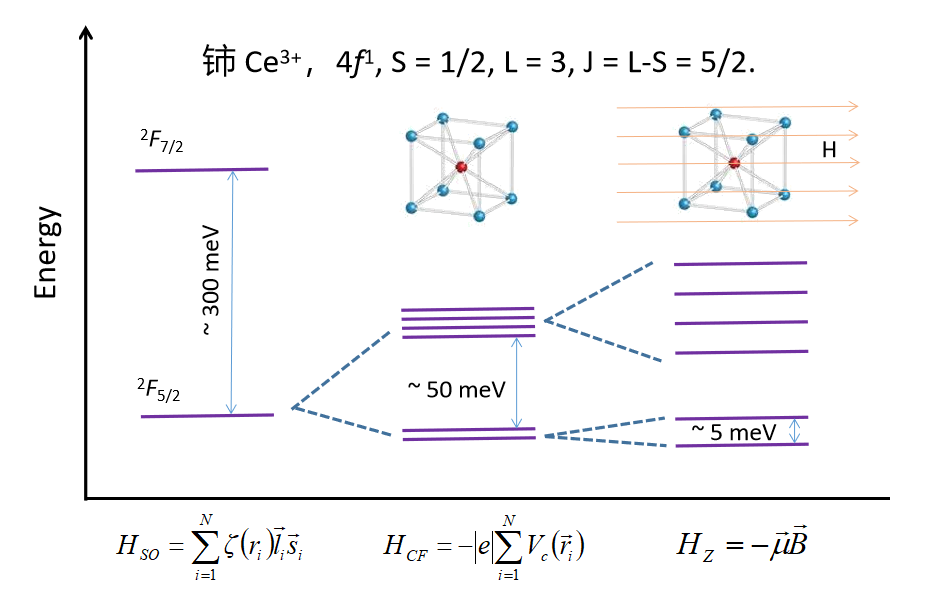
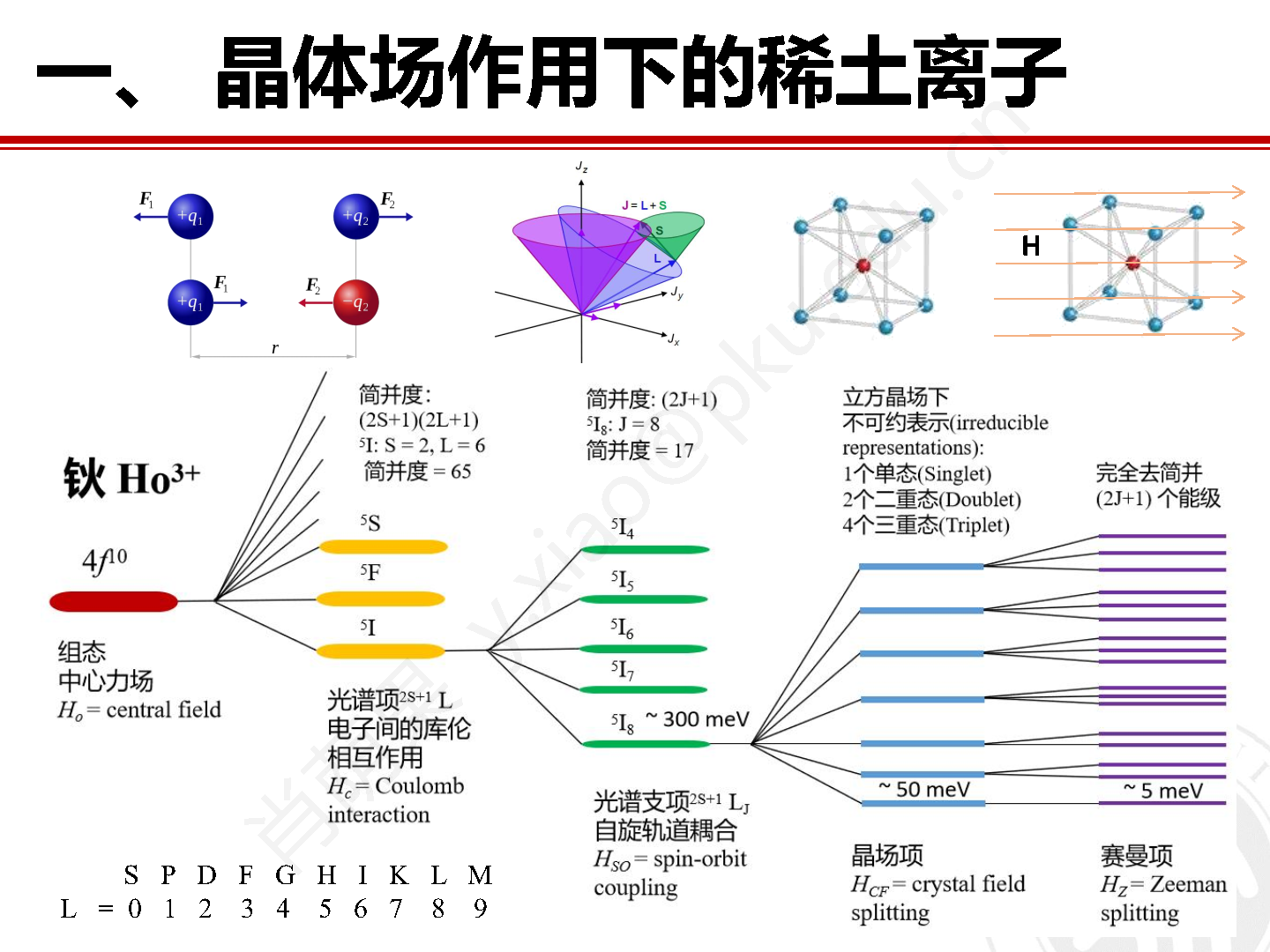
图2 轻稀土Ce3+离子六重简并基态劈裂示意图。
当晶格中的稀土离子被周围配位离子围绕时,配位离子产生的静电场将作用于稀土离子,并导致稀土离子(2j+1)重的简并态部分或全部去简并。对于总角动量为半整数的克莱默离子(Kramers ion),如 Ce3+ (j = 5/2) 和 Nd3+ (j = 9/2) 等,晶场作用下的最小简并度为二重简并。而对于总角动量为整数的非克莱默离子(non-Kramers ion),如Pr3+ (j = 4) 和 Ho3+ (j = 8) 等,晶场作用下可以完全去简并,不过是否能够真正实现完全去简并还要取决于稀土离子所处环境的局域对称性。总之,晶场作用使得稀土离子的多重简并基态发生劈裂,而磁场作用可以使能级进一步去简并,磁场赛曼项(Zeeman term)的本征态与稀土离子的磁量子数有关,如图 2 所示。
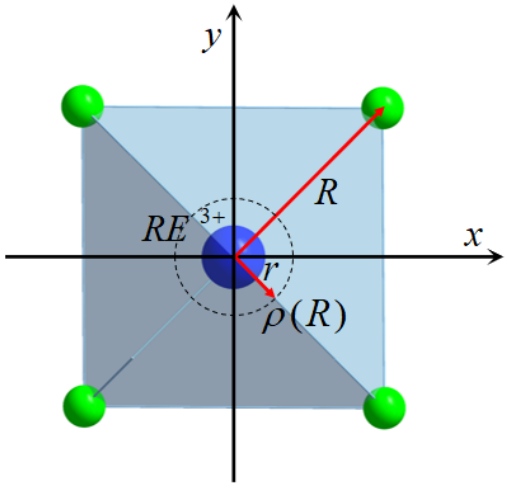
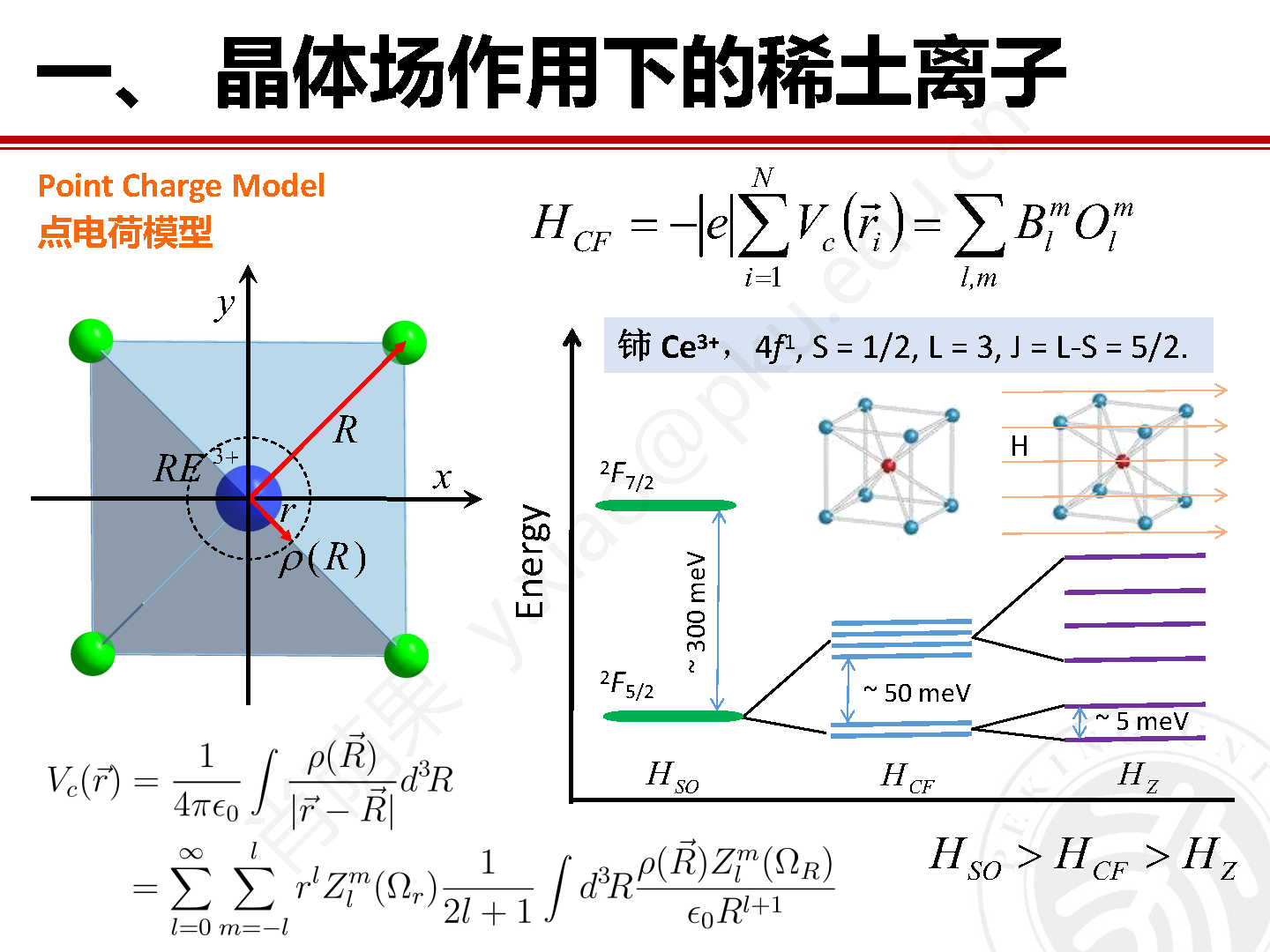
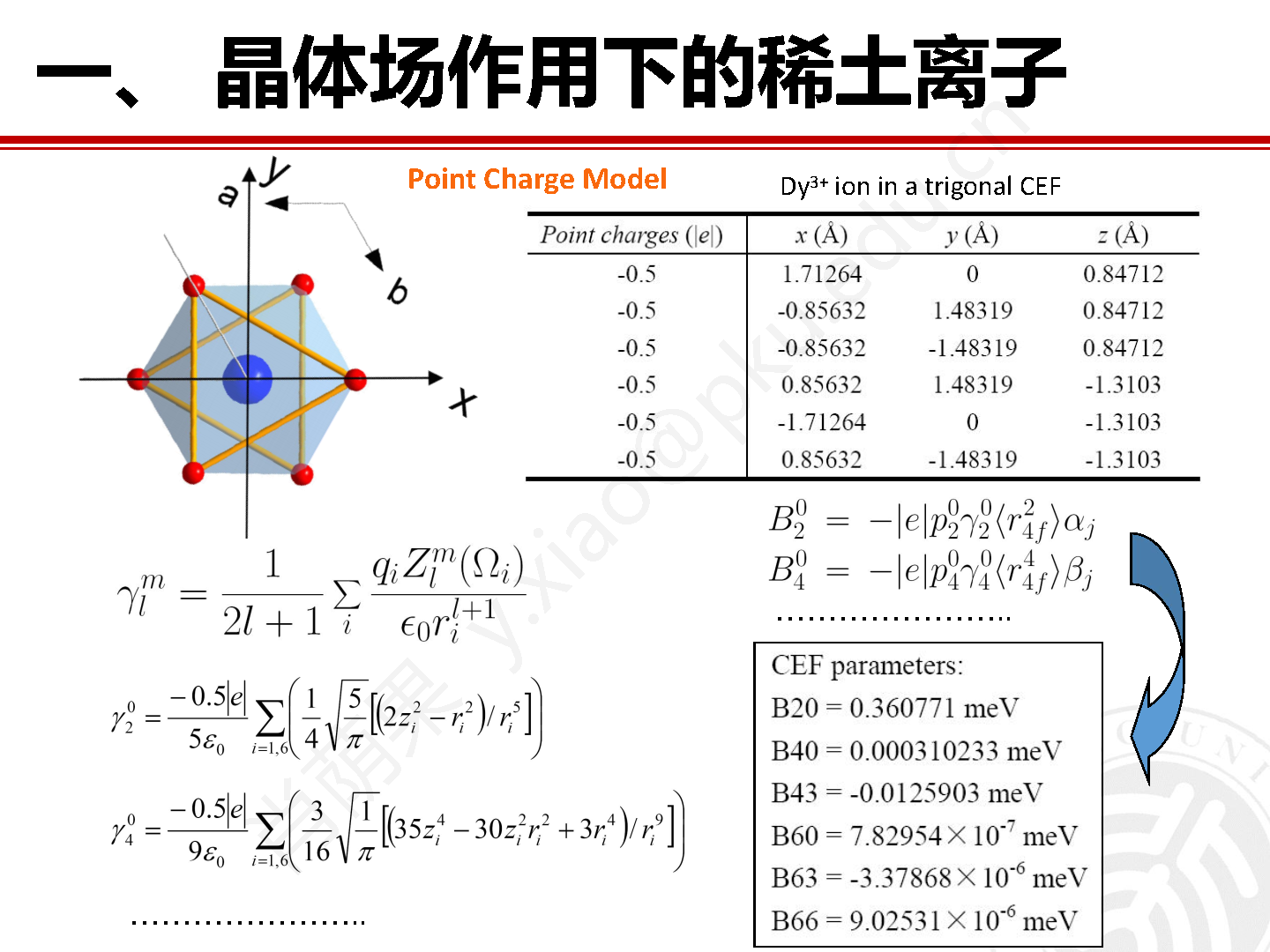
图3 点电荷模型框架下稀土离子和配位离子之间的几何关系。
假设稀土离子的 4f 波函数不和近邻的配位离子波函数重合,并且配位离子带有点电荷 q 时,如图 3 所示,那么稀土离子所受的静电势为:
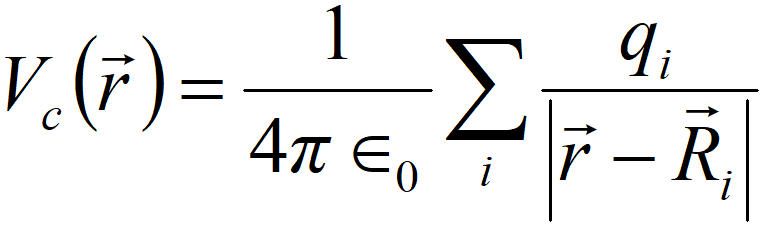
静电势可以通过田谐函数展开并简化之后,带入晶场哈密顿量得到:

上式中B项是晶场参数,O项是史蒂文斯等价算符(Stevens operator equivalents)。其中晶场参数:
![]()
晶场参数由田谐函数多项式系数、稀土离子的径向矩阵元和史蒂文斯因子等组成,因此理论上晶场参数可以通过点电荷模型计算得到。然而点电荷模型具有一定的局限性,准确可靠的晶场参数可以通过非弹性中子散射实验直接测得。不同阶次的史蒂文斯等价算符也有明确的定义,比如:
![]() 。
。
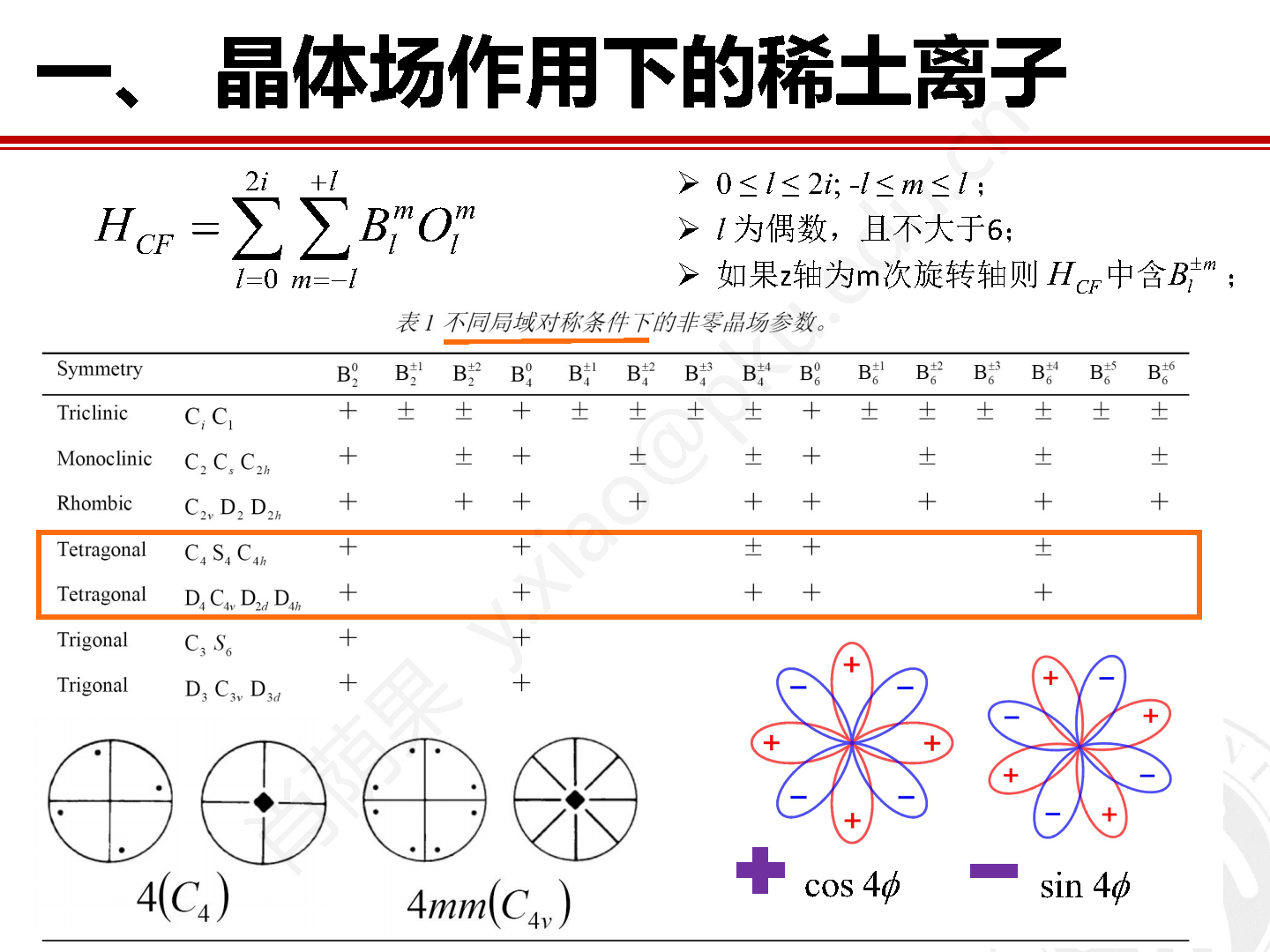
根据晶场理论晶场参数和史蒂文斯等价算符只存在小于等于6的偶数阶,即l = 2, 4 和6。考虑到m = –l ~ l,因此一共可能出现27个不同阶次的晶场参数。真实情况下非零晶场参数的个数主要由稀土离子位点的局域对称性决定。表1中列出了所有晶体学点群对称条件下允许出现的不同阶次的晶场参数。
表1 不同局域对称条件下的非零晶场参数。
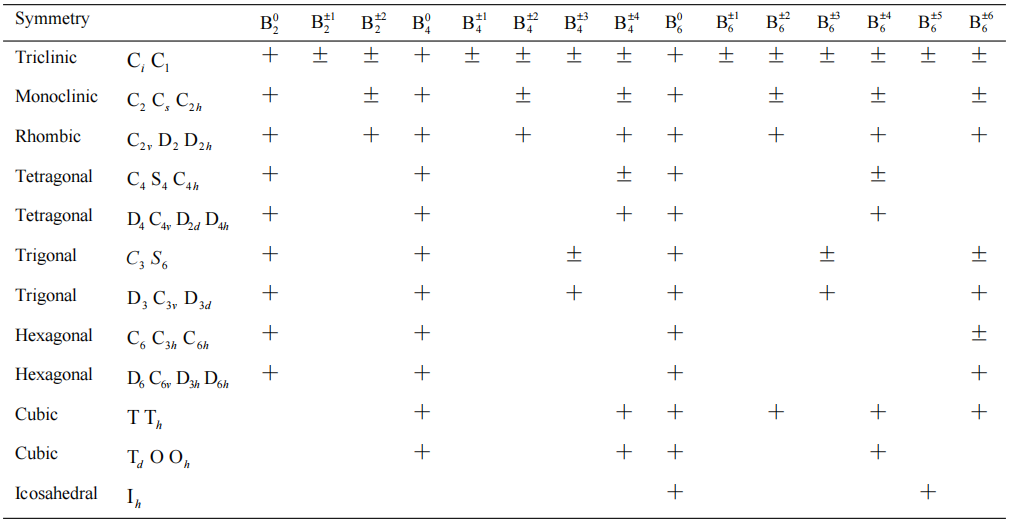
由表 1 可以看出,对称性越高的体系中的稀土离子晶场结构也越简单,需要用来描述晶场结构的晶场参数也越少。例如对于立方体系,不但晶场参数少,而且晶场参数之间还存在等式关系,包括:
![]()
因此立方晶场结构相对简单,甚至可以用参数化的 Lea-Leask-Wolf 图解直接对照得到。
2. 晶场哈密顿量
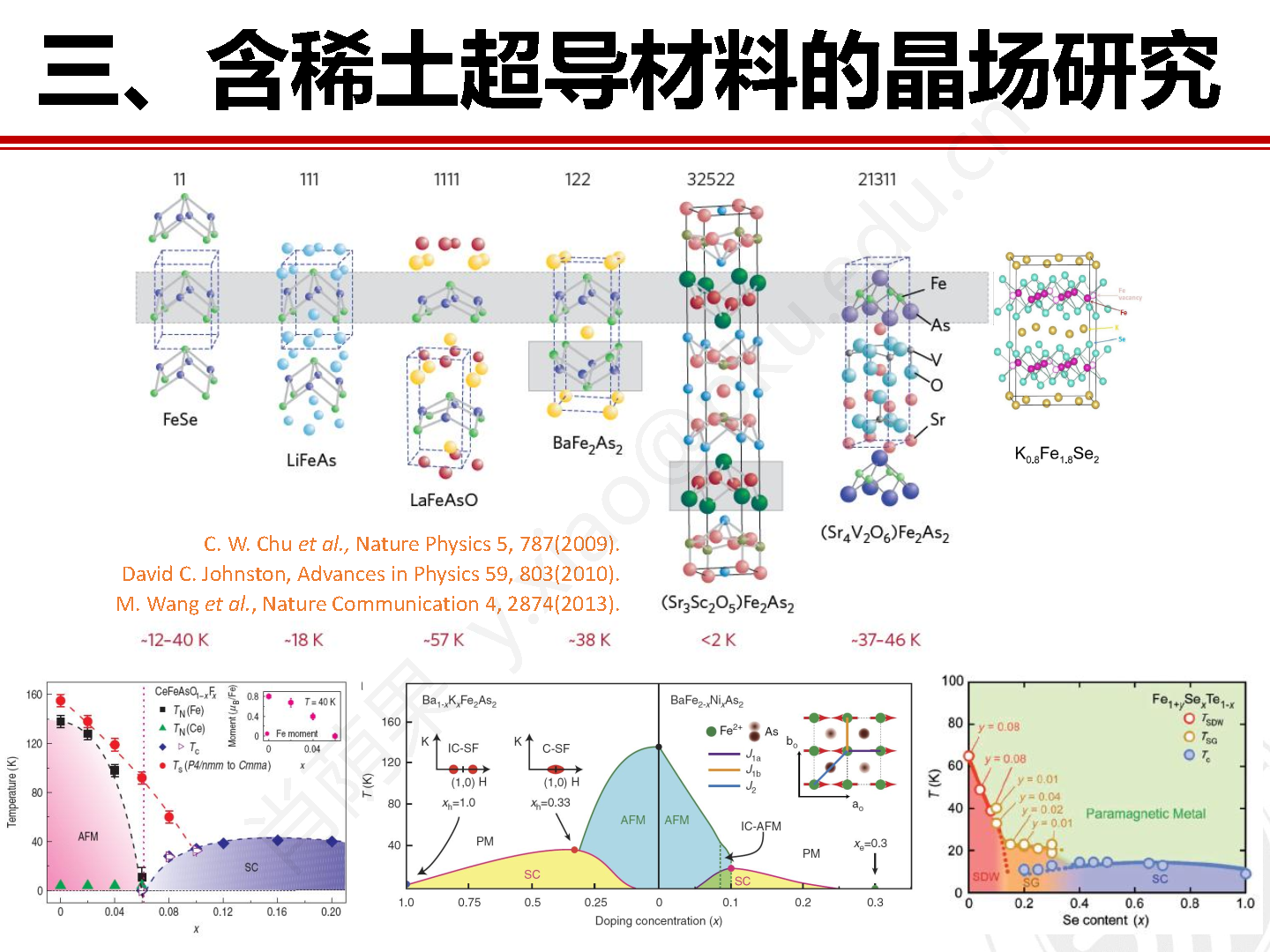
基于晶场理论我们可以得到由晶场参数和史蒂文斯等价算符组成的晶场哈密顿量。通过对矩阵形式晶场哈密顿量的对角化我们就能够得到晶场劈裂的能量本征值和相应的本征态。下面我们以 DyMnO3 化合物中的重稀土离子 Dy3+ 为例简单讨论点电荷晶场模型以及基于晶场理论对稀土离子晶场能级劈裂的分析。首先,已知 DyMnO3 为六方钙钛矿结构,晶胞中有 4b 和 2a 两个Dy3+ 晶位,而两个晶位具有不同的局域对称性,如图 4 所示。

图4 六方钙钛矿 DyMnO3 中 Dy3+ 晶位的局域对称性。
作为示例我们在这里主要讨论 2a 位置 Dy3+ 的晶场能级劈裂。根据表 1,可以得到其晶场哈密顿量:
![]()
根据史蒂文斯等价算符的定义,有:

该体系中等价算符主要由 Jz 项以及阶梯算符 J+ 和 J– 项组成,根据定义有:
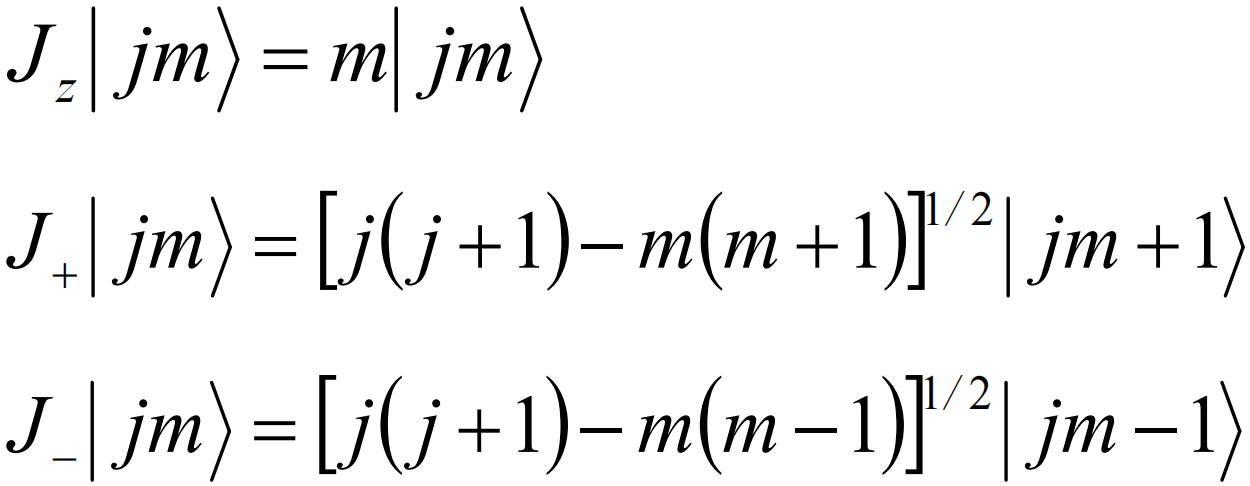
![]()
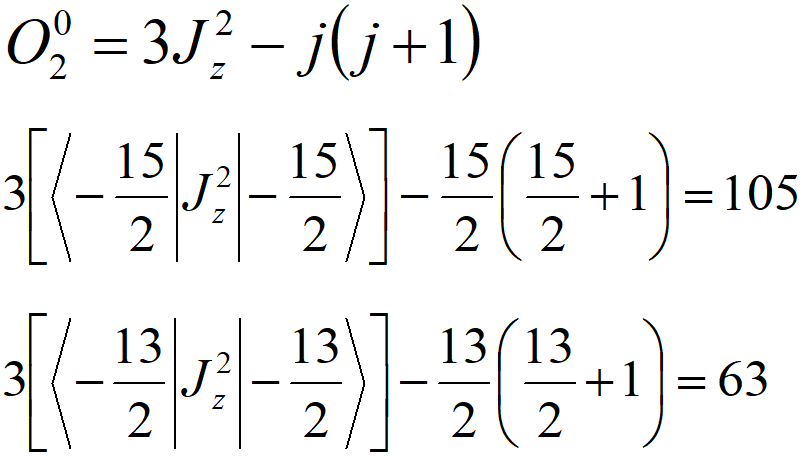
以下计算略…………………
以此类推就能够得到所有的矩阵元素。Dy3+ 离子的 j = 15/2,因此得到的是一个 16×16 矩阵。再结合对应阶次的晶场参数,我们就能够得到矩阵形式的晶场哈密顿量:

由上式可以看出,除了史蒂文斯等价算符之外,我们还需要得到6个不同阶次的晶场参数。如前文所述,晶场参数可以通过近似的点电荷模型计算得到。对于DyMnO3中2a位置的Dy3+离子来说,其最近邻由6个带电的O2-离子组成,考虑到价态平衡,每个O2-离子作用于Dy3+离子的有效电荷为-0.5|e|。图5中给出了Dy3+离子位于三方晶场的局域配位环境。

图5 六方钙钛矿 DyMnO3 中2a晶位 Dy3+ 离子的局域配位环境。
由:
![]()
可以计算得到所有的晶场参数:
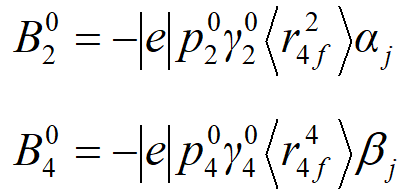
以下略…………………
最后得到:
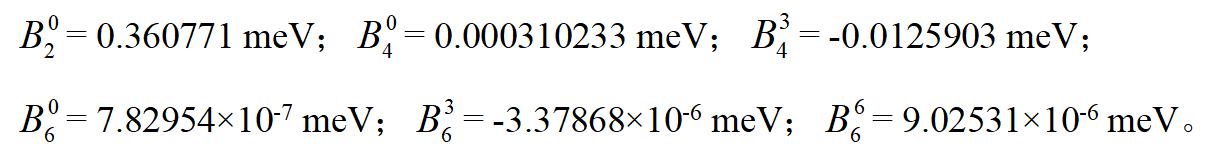
采用这些计算晶场参数,将晶场哈密顿算符作用于波函数,然后再经过对角化就能得到与晶场劈裂能对应的本征能量和本征矢量。
![]()
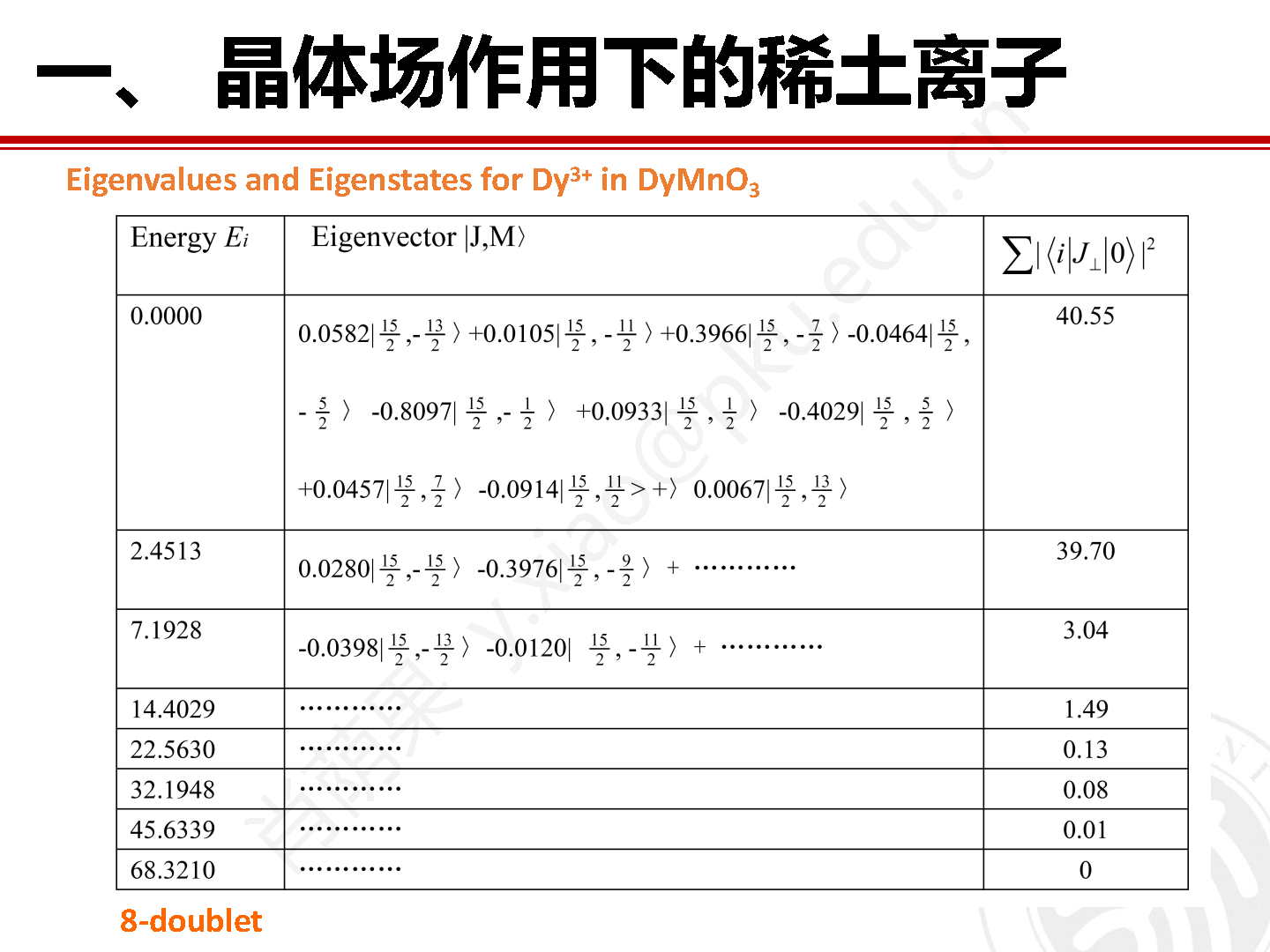
表 2 列出了本征能量和本征矢量以及每个激发态和基态之间矩阵元素的平方和。由于 Dy3+(J = 15/2) 是克莱默离子,因此在晶场作用下得到 8 个二重简并能级。不同的晶场本征态通常用不可约表示 Γi 来做标识。
表2 对角化晶场哈密顿量矩阵后得到的本征值和本征矢量。

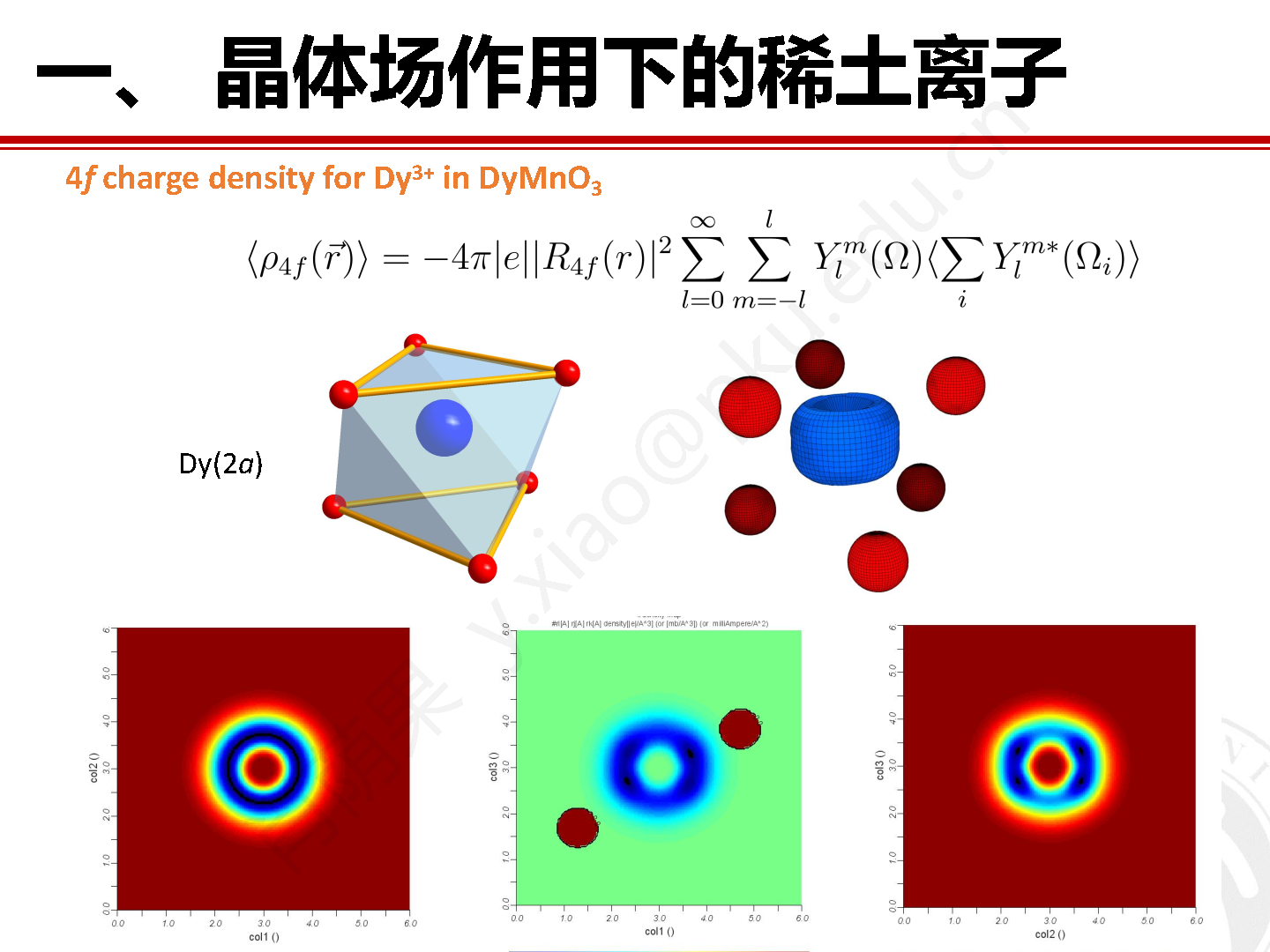
通过田谐函数组合表达并叠加所有的晶场态,我们还能够得到Dy3+的4f电子各向异性的电荷密度分布,如图6所示。
![]()

图6 六方钙钛矿 DyMnO3 中 2a 晶位 Dy3+ 的 4f 电子的电荷密度分布。
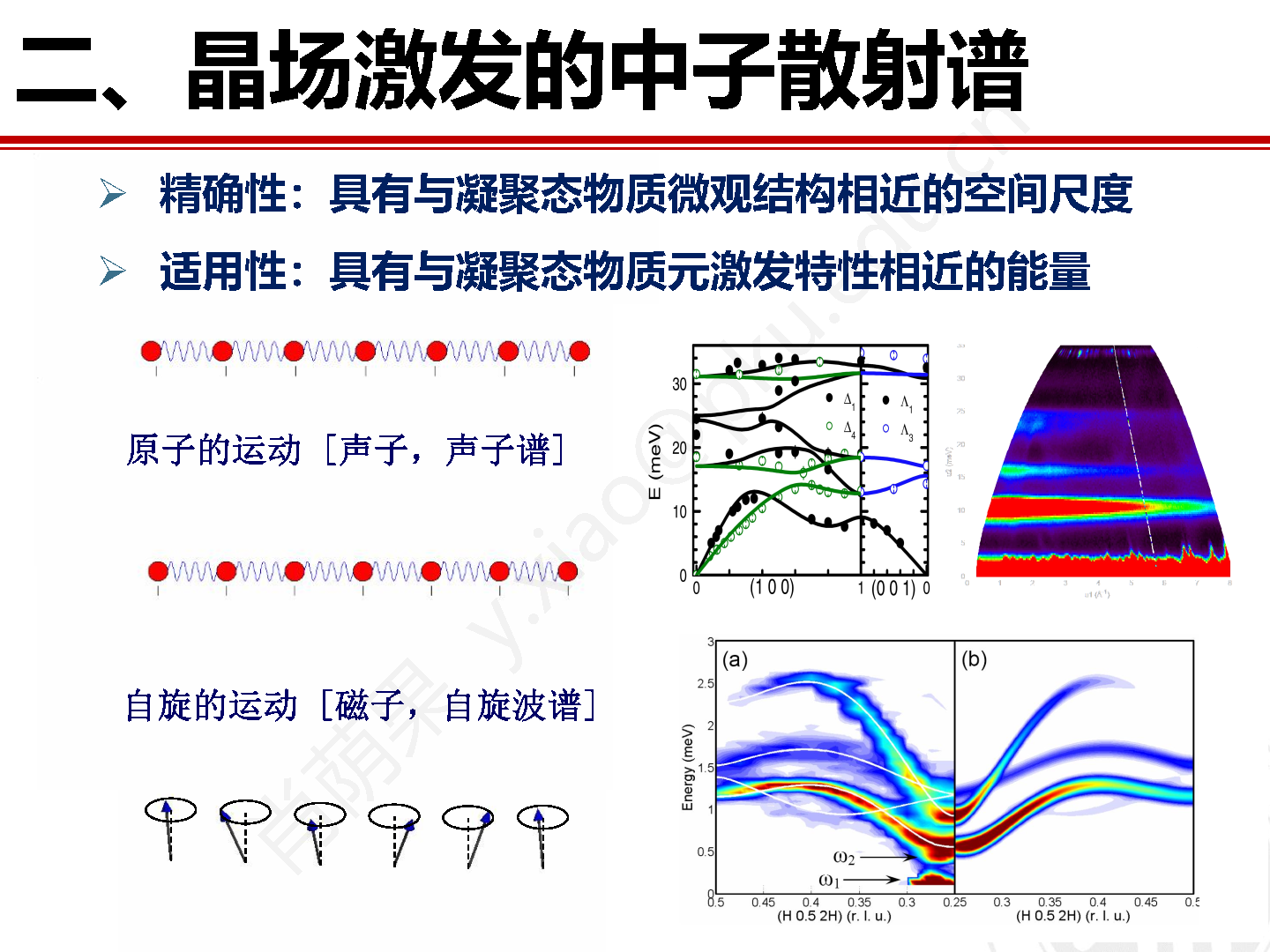
3. 晶场激发的中子散射谱
在偶极矩近似条件下,中子会受 4f 电子简并态作用发生弹性散射,同时也能够通过吸收或释放一定的晶场跃迁能量被激发或者退激发,即发生非弹性散射。显然,晶场的中子散射本质上是一个磁散射过程。此外,由于晶场劈裂是单个离子发生的纯局域效应,因此如果不被其它相互作用影响的话,晶场激发为单离子激发并具有无色散激发的特点。
晶场激发的非弹性中子散射截面为:
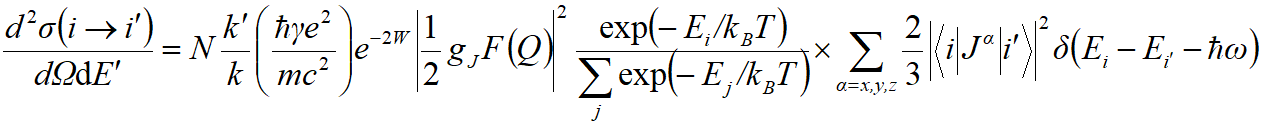
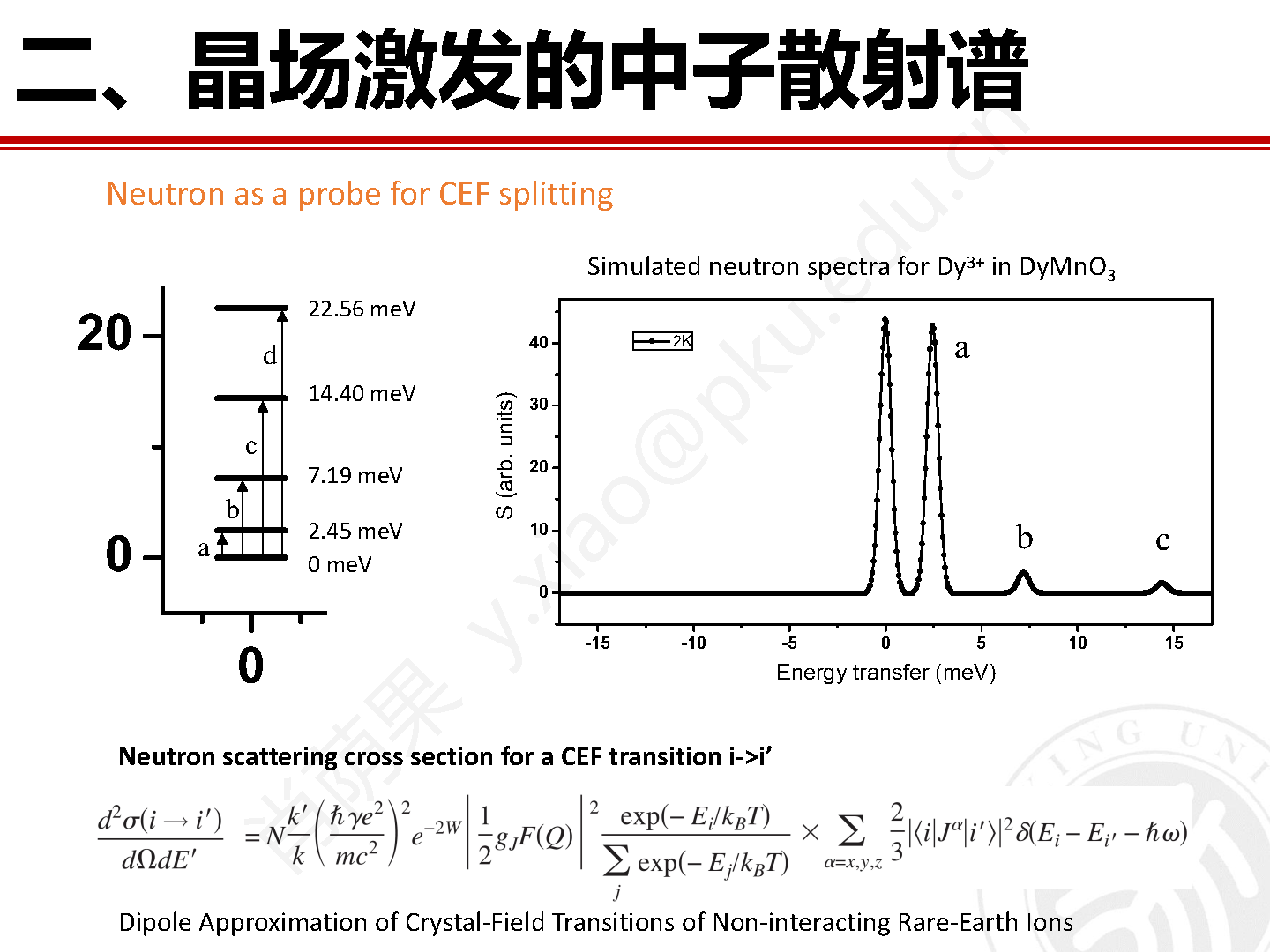
由上式可以看出,虽然晶场激发没有色散的特点,但是散射截面中包含形状因子,因此具有明显的 Q 依赖特征。此外,晶场激发的非弹性中子散射谱还会表现出很强的温度依赖特点。我们继续以 DyMnO3 为例,在 2K 时的计算非弹性中子散射谱如图 7 所示。
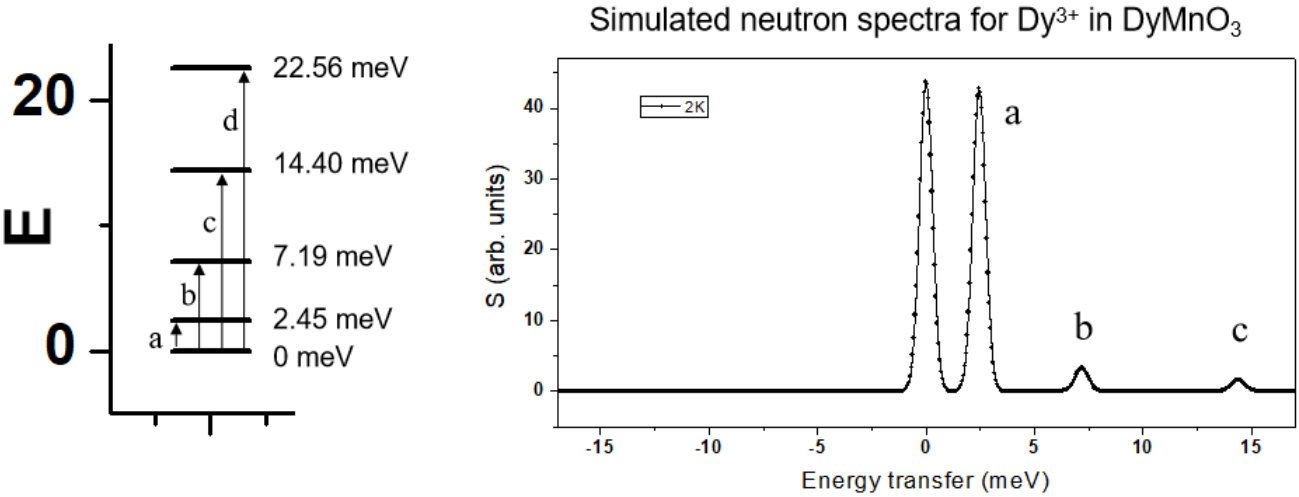
图7 六方钙钛矿 DyMnO3 在 2K 时的晶场示意图和计算非弹性中子散射谱。
中子谱中的峰对应不同晶场能级之间的跃迁,峰的强度决定于晶场矩阵元素的平方和。图 7中还可以看出,2K 的中子谱中晶场激发信号主要集中在能量损失一侧,而能量获取的一侧没有激发信号。能量获取强度和能量损失强度之间存在平衡关系,即:
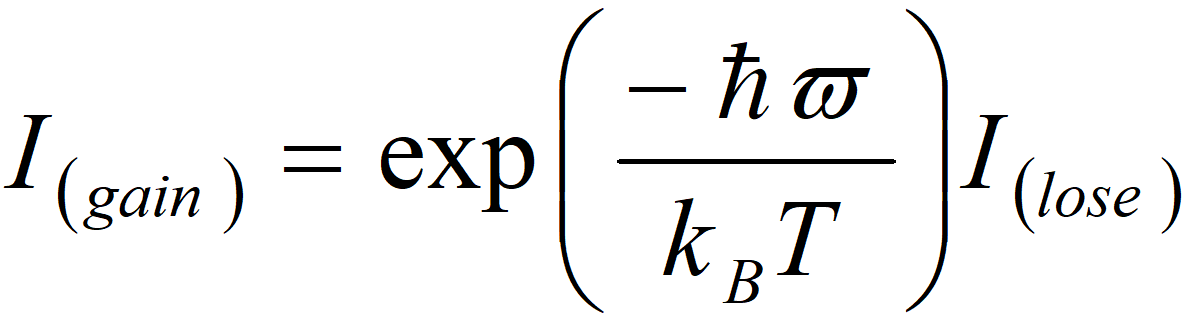
随着温度升高,能量获取一侧的信号也将逐渐增加,代表退激发的过程,如图 8 所示。同时,随着温度升高,激发态能级之间跃迁的概率也大大增加,从而导致除了基态到激发态之间跃迁之外的不同激发态能级之间跃迁的晶场激发信号的出现。图 8 为不同温度条件下的晶场激发中子谱,不同类型晶场激发峰随温度的变化规律清晰可见。因此在晶场激发的非弹性中子散射实验中,充分利用晶场峰不同的变化规律就可以判断晶场激发的类型,并据此推导得到体系清晰的晶场激发图像。
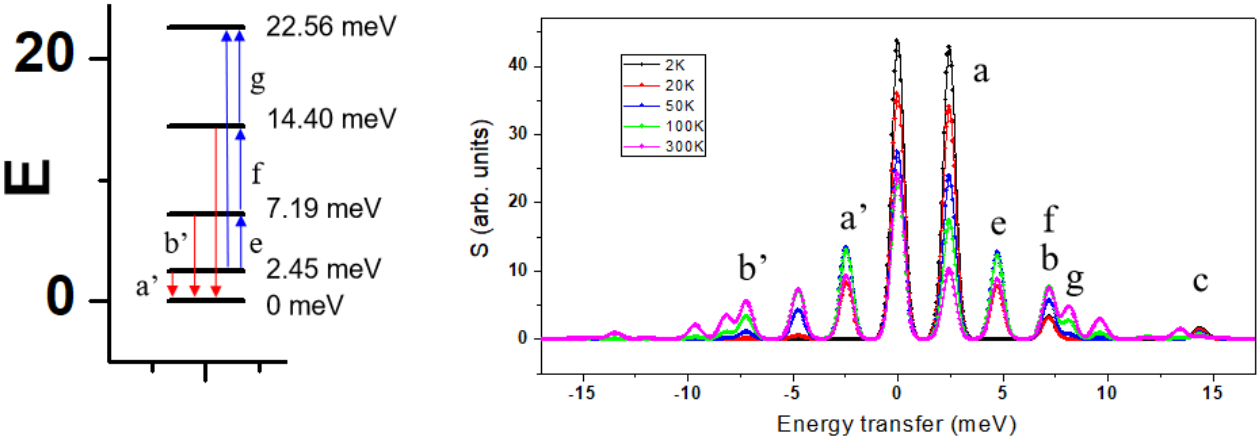
图8 六方钙钛矿 DyMnO3 在不同温度条件下的晶场示意图和计算非弹性中子散射谱。
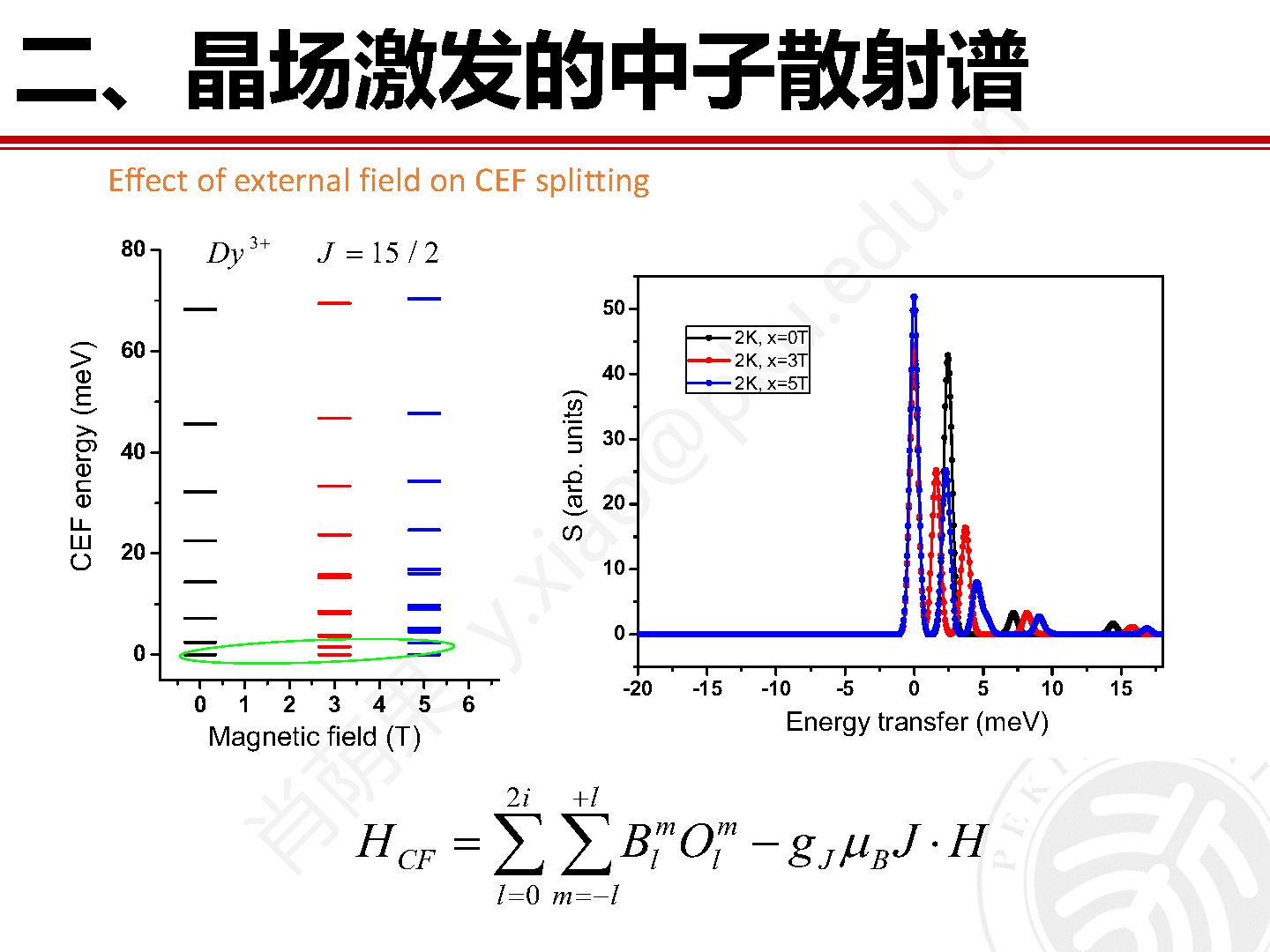
前文提到,磁场作用可以使晶场能级进一步去简并。这里磁场可以是外磁场也可以是由体系中其它磁子晶格产生的内磁场。图 9 展示了外磁场对 DyMnO3 中 Dy3+ 晶场进一步去简并的效果。
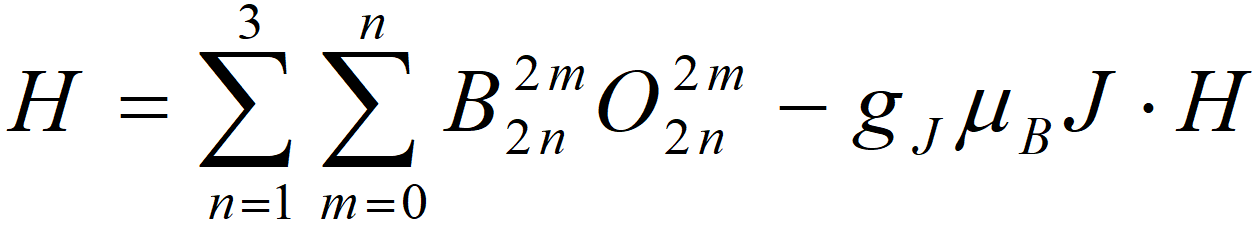

图9 六方钙钛矿 DyMnO3 在不同外磁场作用下的晶场示意图和计算非弹性中子散射谱。
4. 非弹性中子散射实验研究
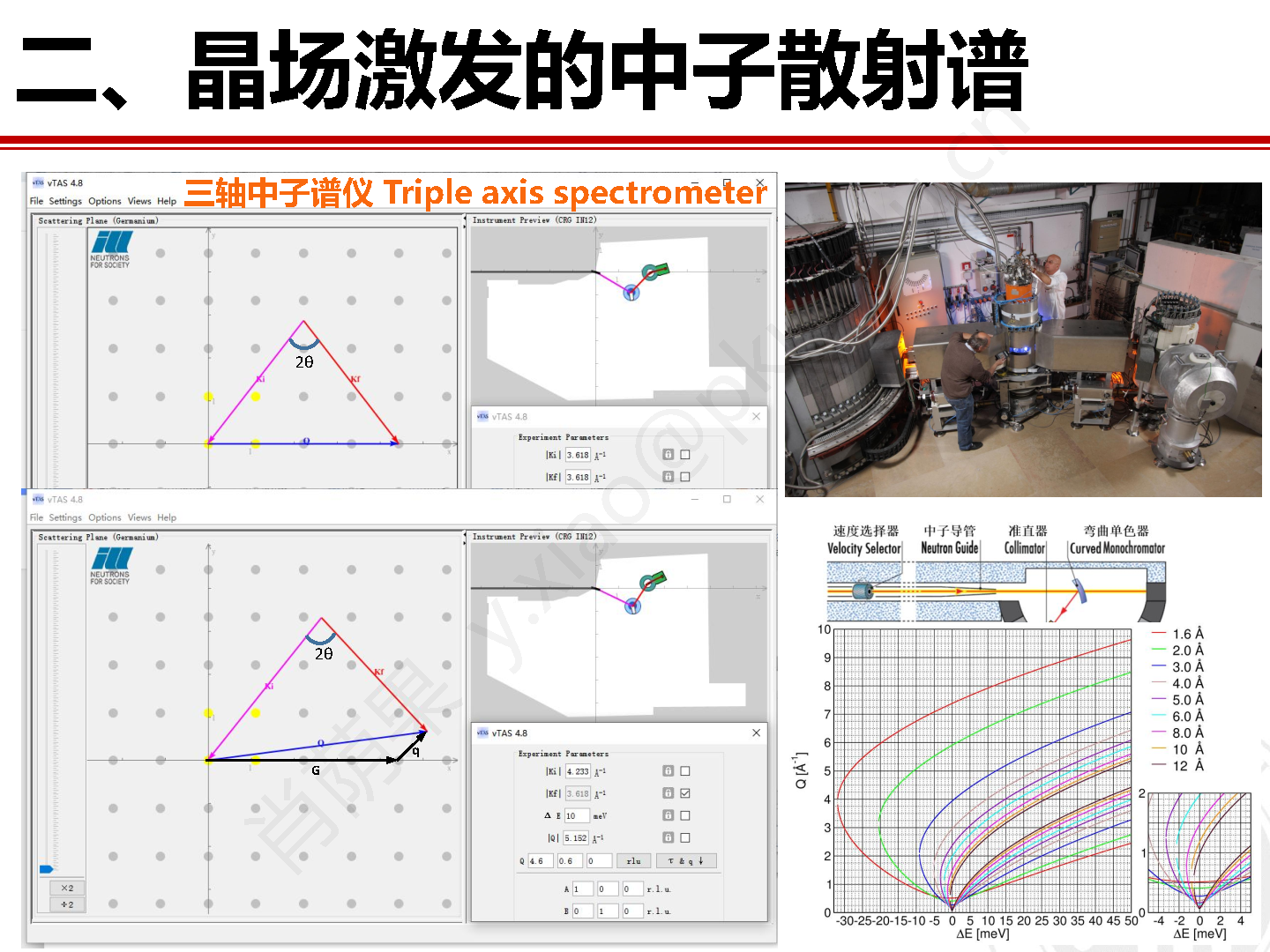
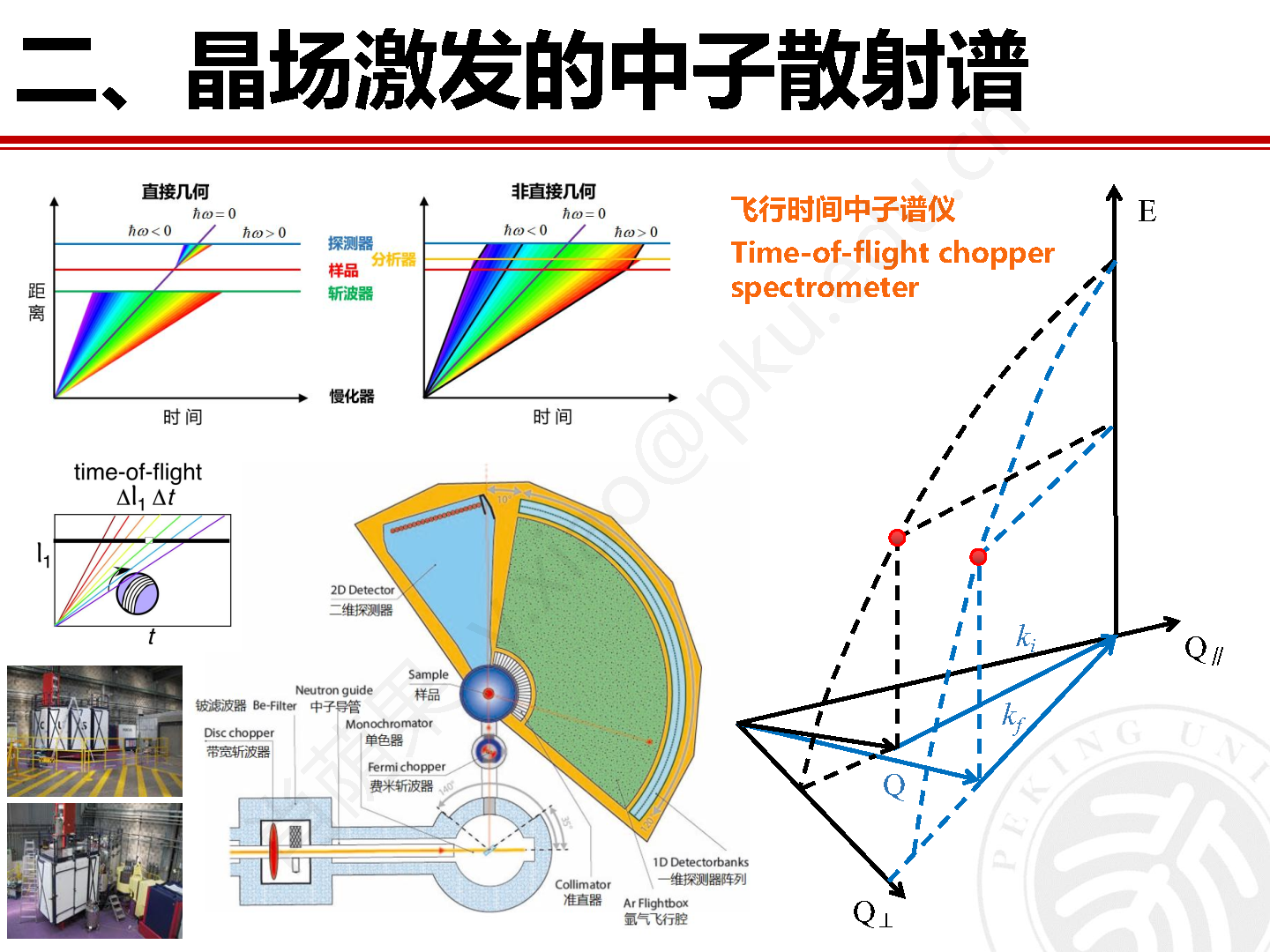
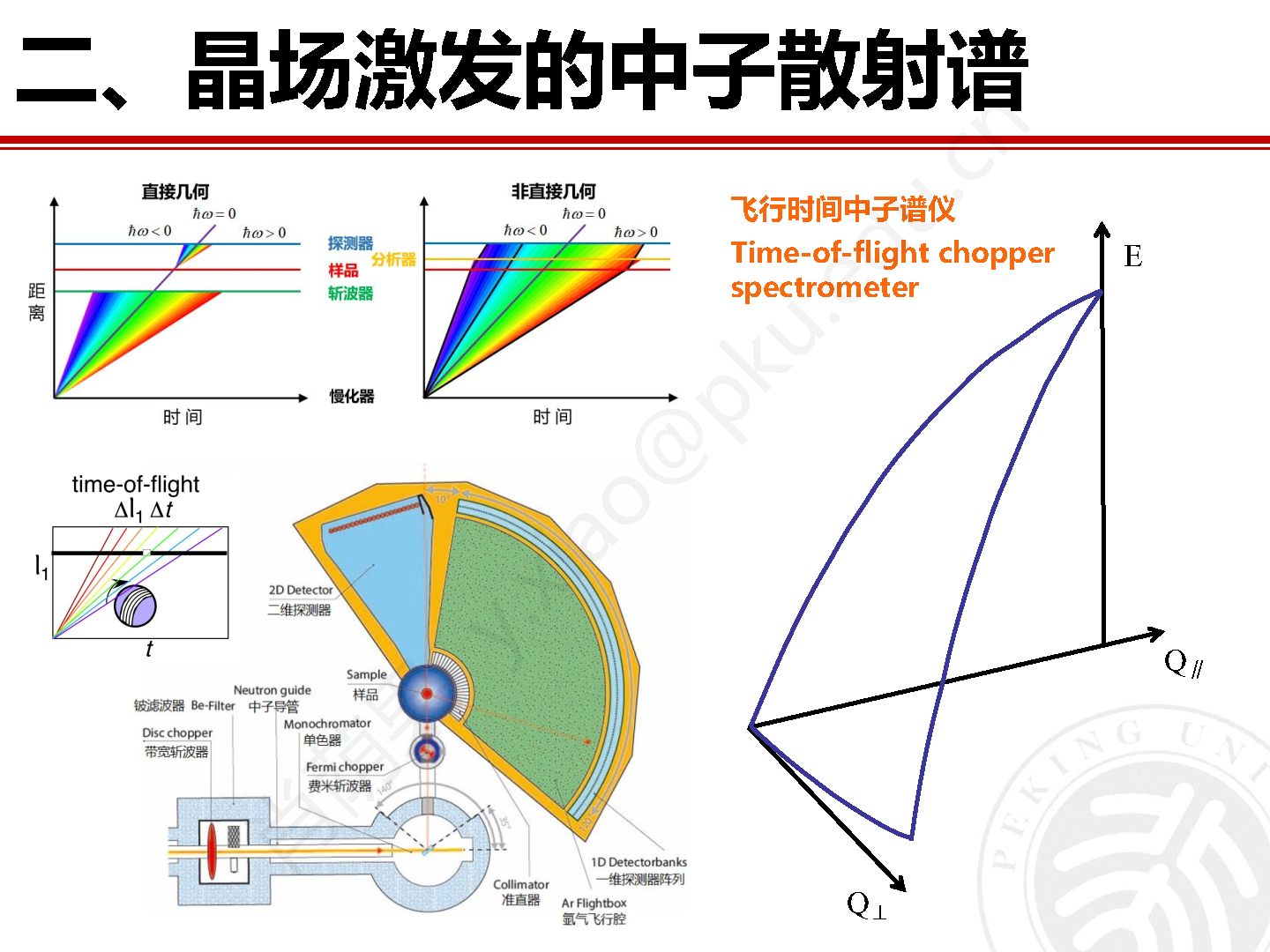
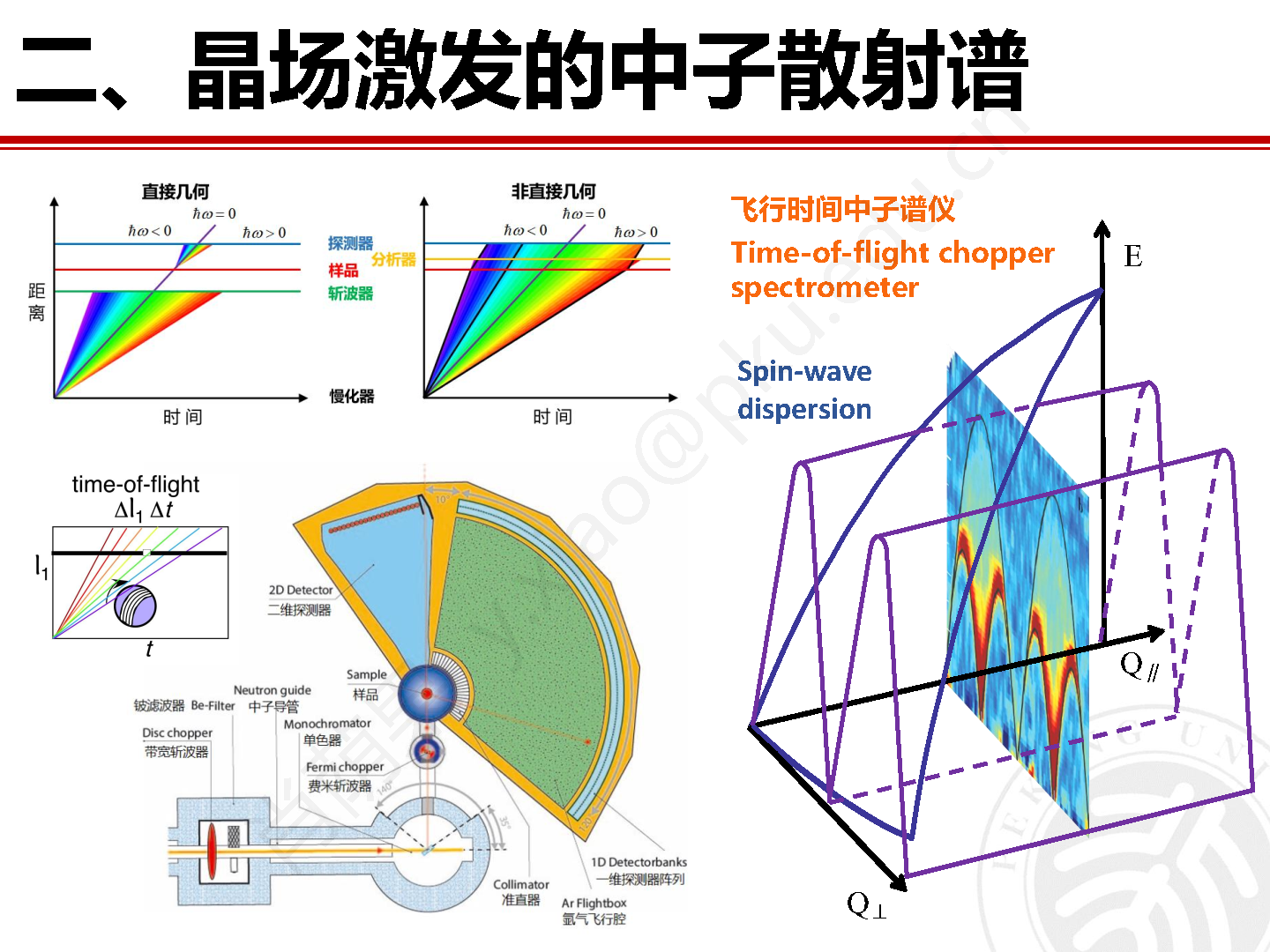
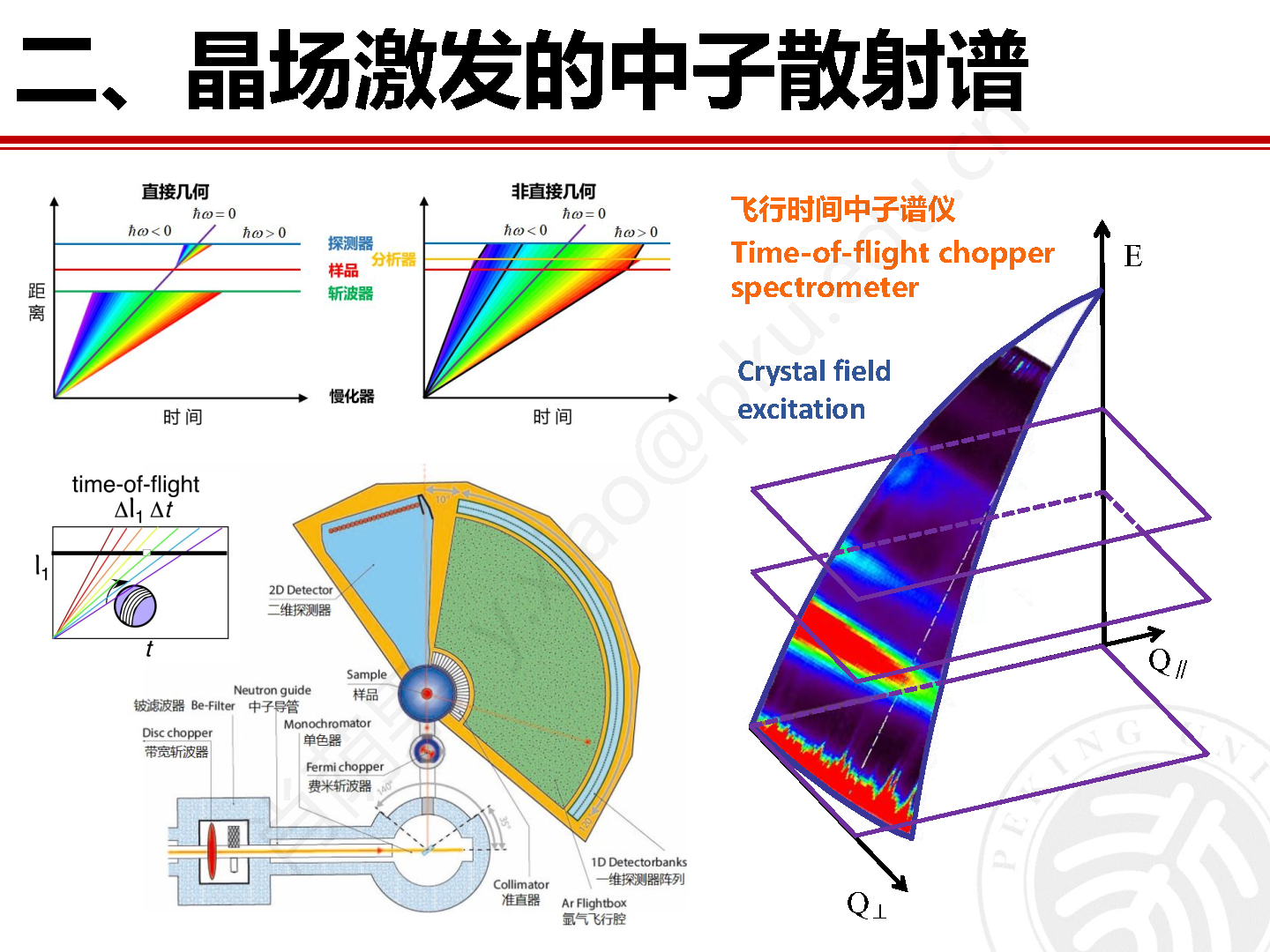
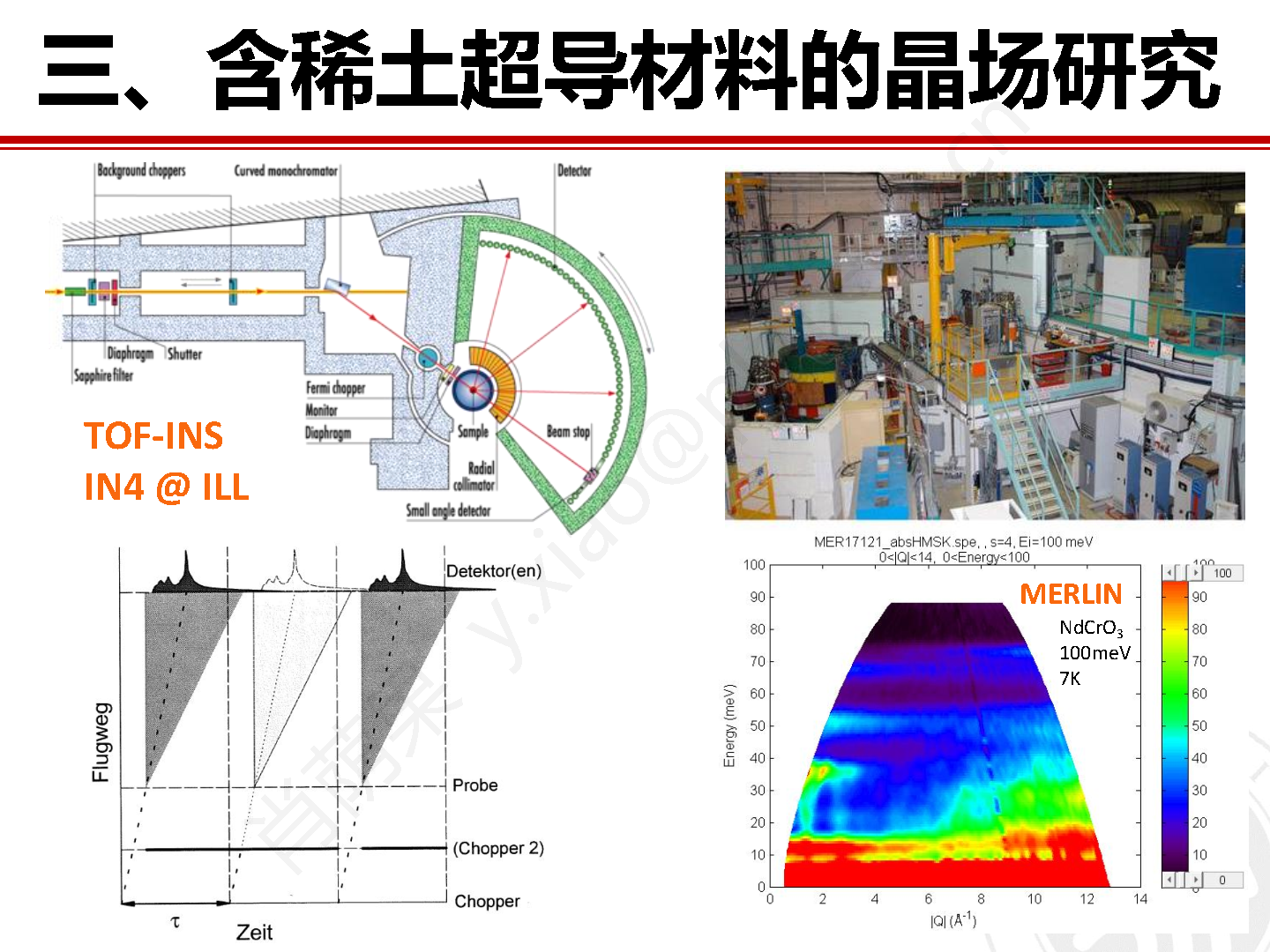
在针对材料晶场激发的研究方法方面,最高效最便捷的方法是利用晶场激发谱无色散的特点,采用飞行时间非弹性中子谱仪对粉末样品展开实验研究。位于瑞士保罗谢勒研究所(PSI) 的瑞士散裂中子源(SINQ)上的直接几何飞行时间冷中子非弹谱仪FOCUS就非常适合展开晶场激发的研究工作。图10为FOCUS的结构示意图和实物图。作为直接几何非弹谱仪,入射中子首先通过单色器和费米斩波器被单色化,随后和待测样品发生散射后又被不同散射角度的探测器探知。探测器记录散射中子的角度位置以及到达探测器的时间,并据此得到散射中子的波矢和能量。
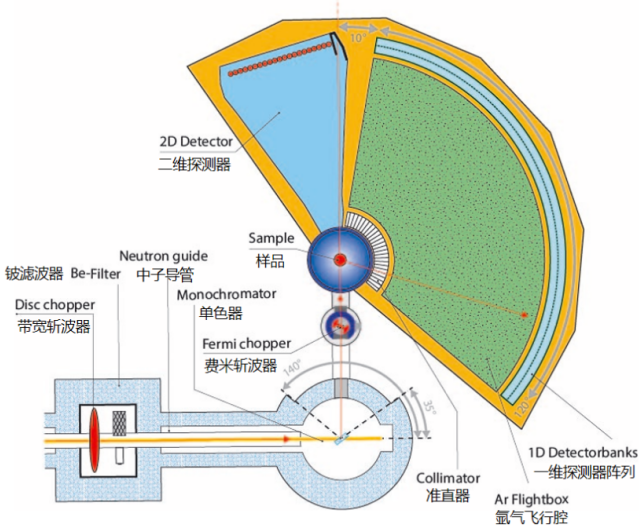

图10 瑞士SINQ的直接几何非弹中子谱仪 FOCUS 的结构示意图和实物图。
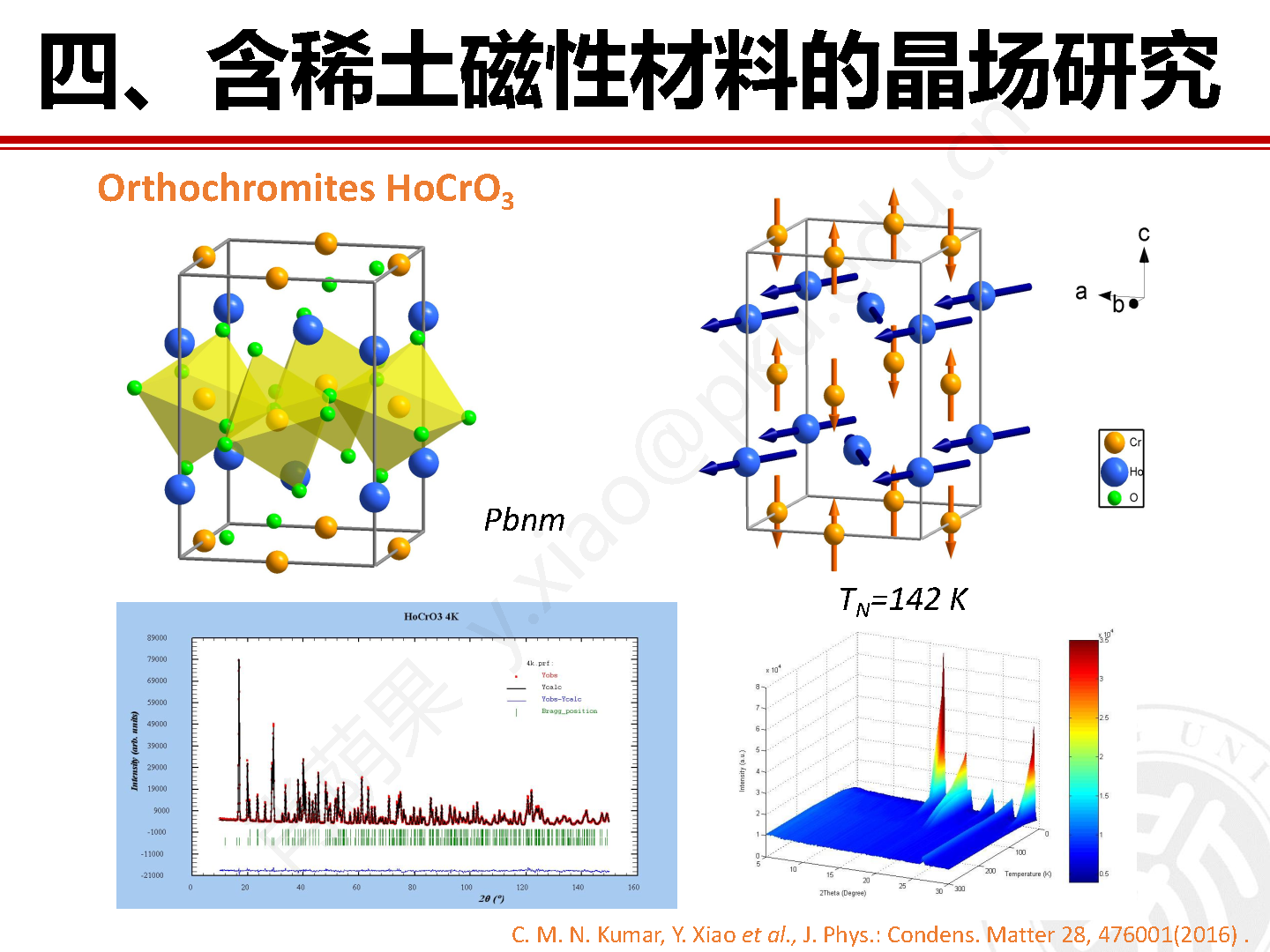
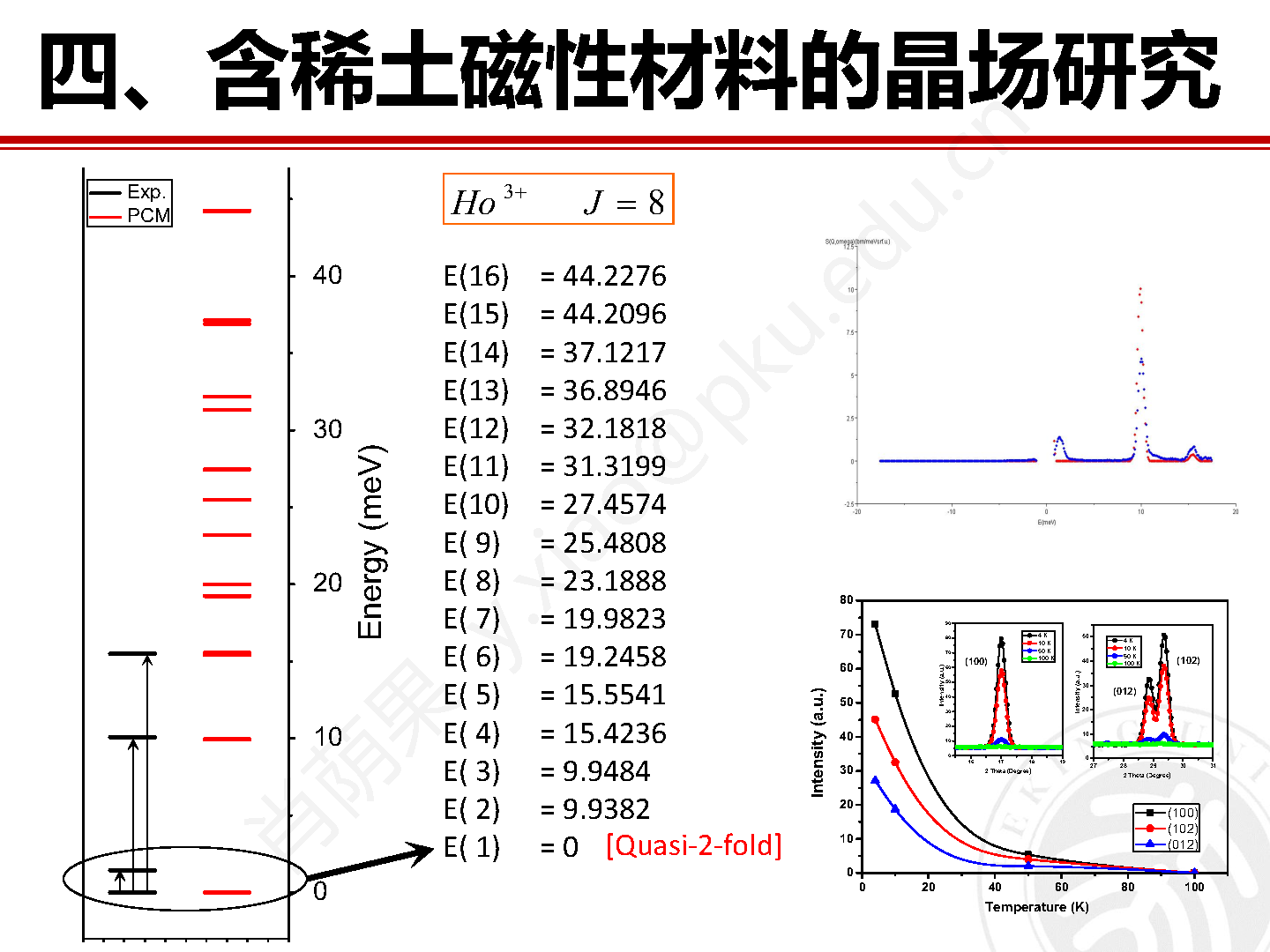
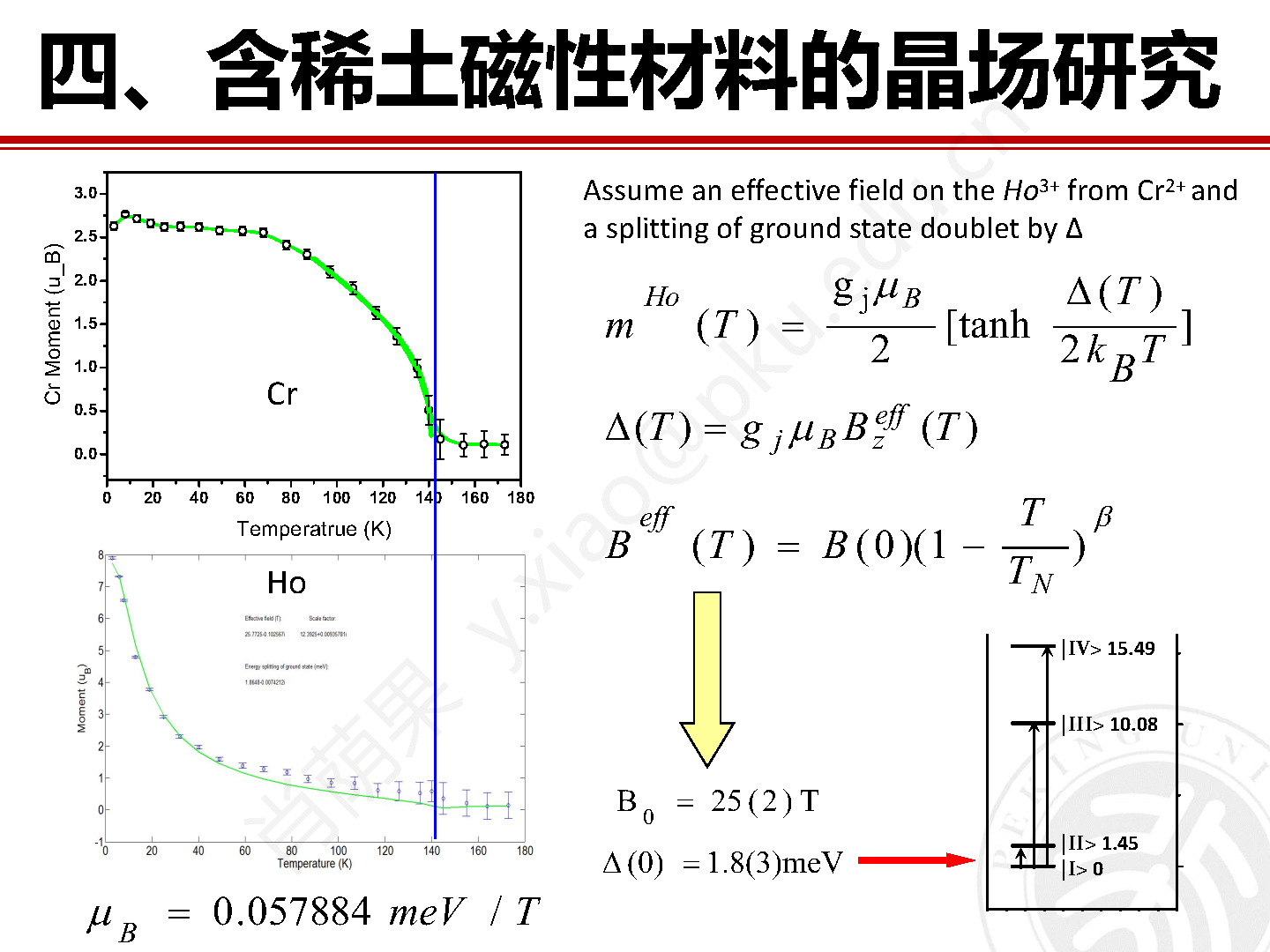
图 11 为在 FOCUS 上采集的 HoCrO3 样品的低能晶场数据,从数据中可以看出,Ho3+ 的晶场信号出现在固定的能量值,信号强度随着 Q 的增加略有衰减。沿着 Q 选段积分后就能得到可以用于晶场分析的二维晶场激发谱。该实验重点关注的是 HoCrO3 中磁性 Cr2+ 离子的磁有序作用于 Ho3+ 上的有效分子场引起的低能晶场激发,因此选用的是冷中子非弹谱仪。如果关注高能晶场激发可以选择能量覆盖范围更宽的热中子非弹谱仪。
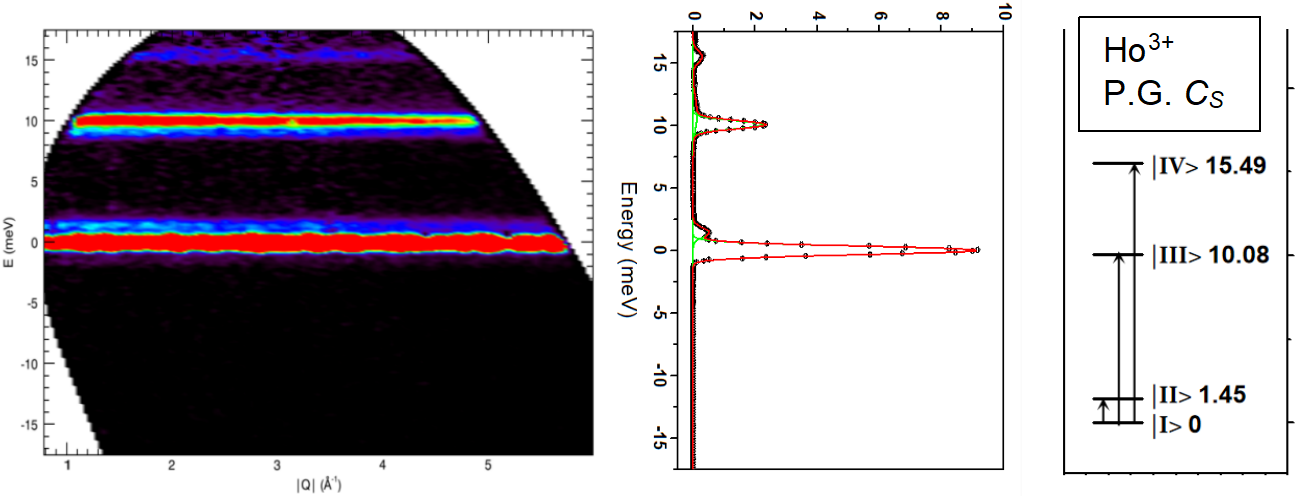
图11 在直接几何非弹中子谱仪 FOCUS 上采集的 HoCrO3 样品的低能晶场激发数据。
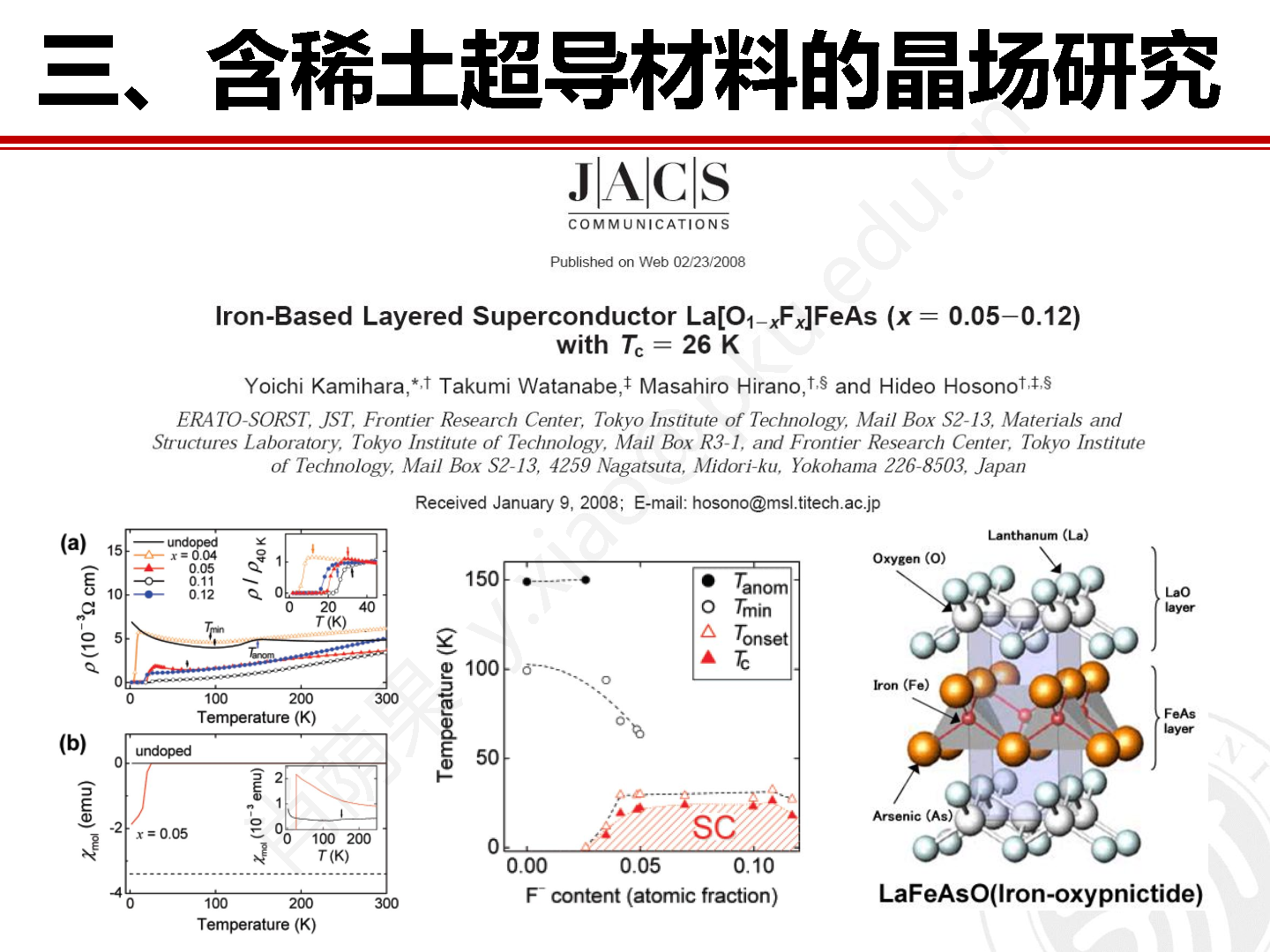
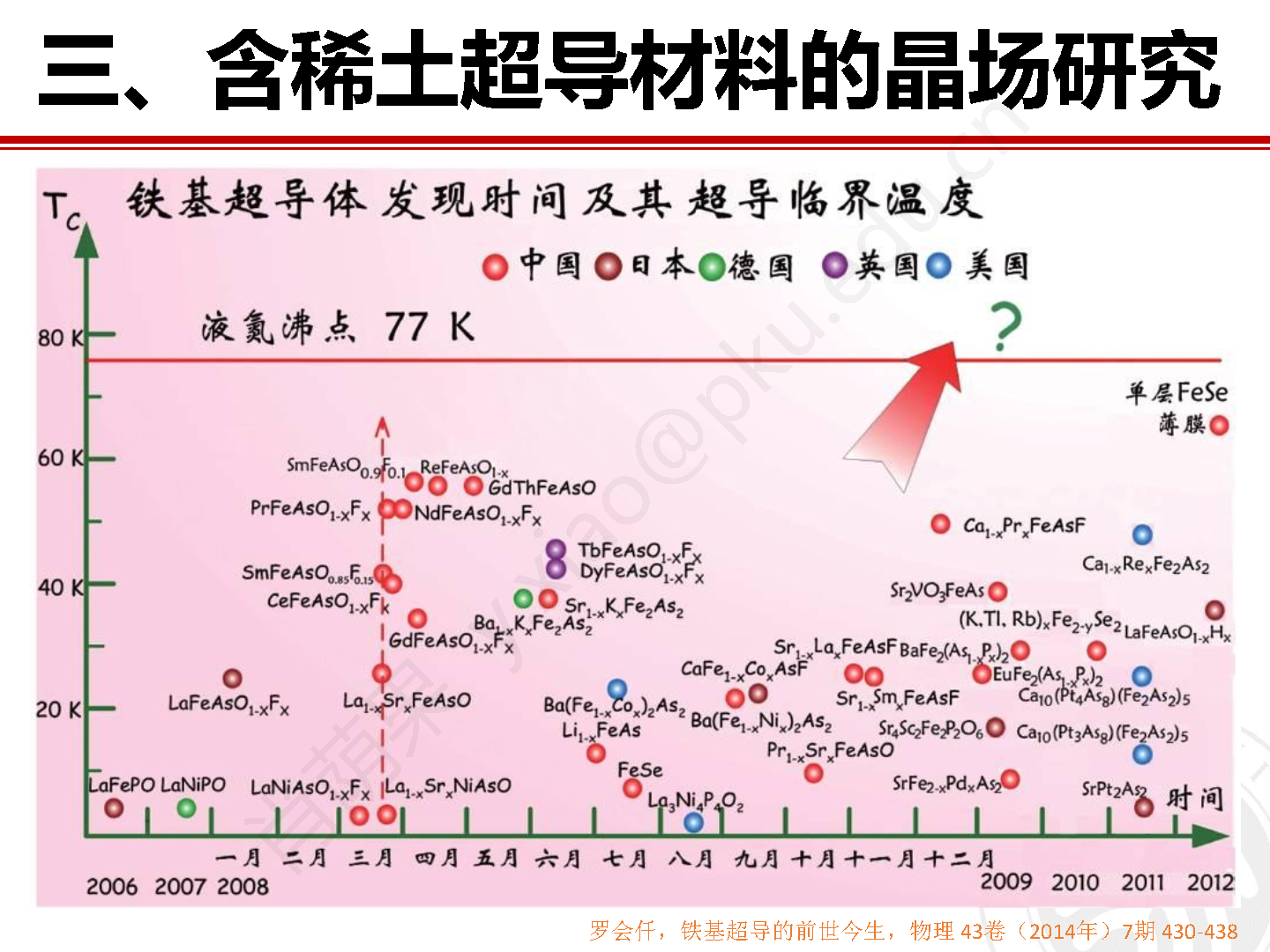
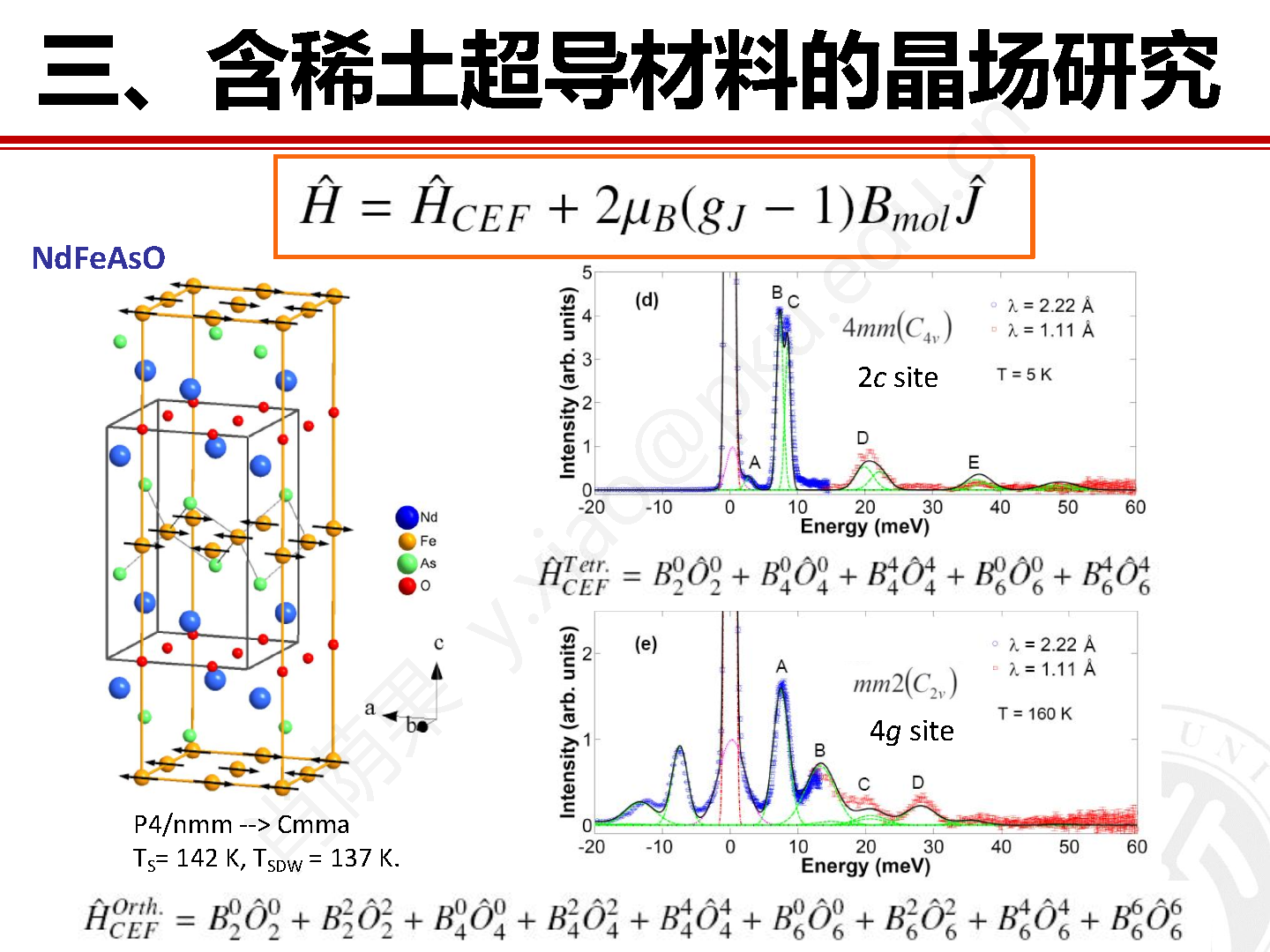
含有稀土钕元素的 NdFeAsO 是一种铁基超导母体相,用一定量的氟替代母体相中的氧能够诱导出现 50 K 以上的超导转变温度。虽然稀土元素的作用不是体系出现非常规高温超导的关键,但是稀土磁性和过渡金属磁性之间的相互作用毫无疑问是决定体系结构和物性的不可忽视的因素。因此,从实验角度直接探测稀土离子 Nd3+ 的晶场结构有助于加深我们对双磁子晶格相互作用以及体系物理性能的理解和认识。我们在法国格勒诺布尔的劳厄朗之万研究所(ILL) 的直接几何热中子飞行时间谱仪 IN4C 上对 NdFeAsO 粉末样品展开晶场激发研究工作。

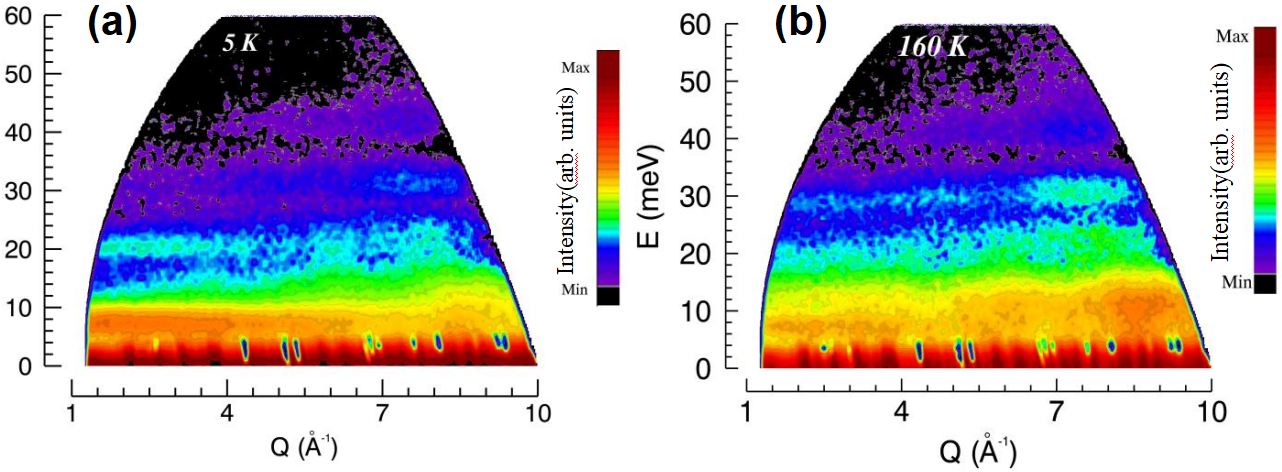
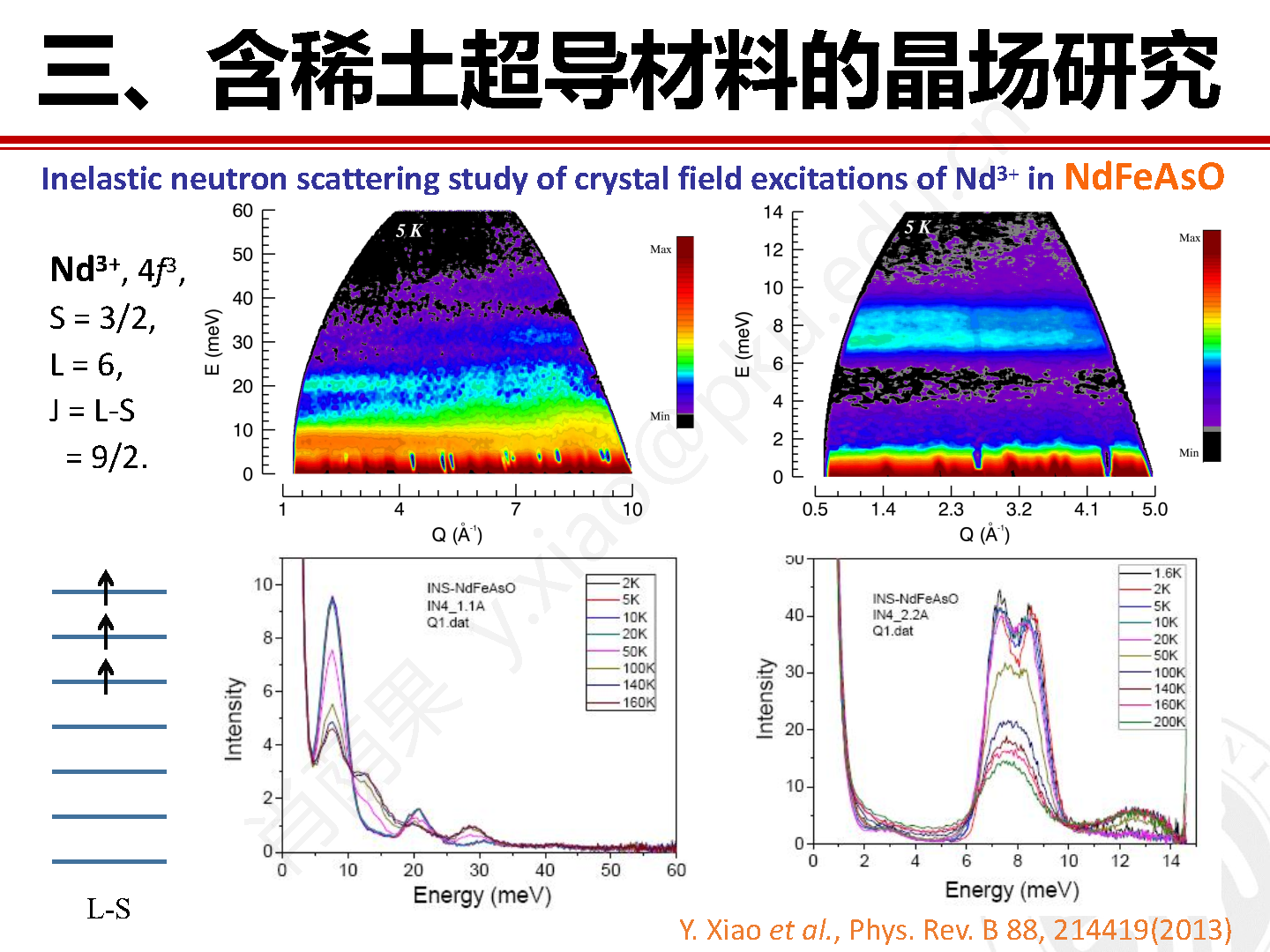
图12 非弹性中子实验测得的稀土化合物 NdFeAsO 在 5 K 和 160 K 的S(Q,ω)图。
为了兼顾能量分辨率和 Q 值覆盖范围,我们选择 λi = 1.11 Å 和 2.22 Å 两种入射中子波长,并且使用低温恒温器覆盖 1.6 K 到 200 K 的温度范围。 图 12(a) 和 (b) 为经过玻色因子校正的 NdFeAsO 在 5 K 和160 K 的非弹性中子谱。需要指出的是在 5 K 谱图的能量损失一侧,非弹信号不但包括了晶场激发,而且还包括自旋波激发和声子激发信号。由于自旋波激发信号相对较弱所以可以忽略这部分的贡献,而主要考虑占主导的声子激发和晶场激发。由于该实验中采用的是非极化中子,所以不能直接对这两项分别来自核散射和磁散射的贡献进行直接区分。但是这两种激发具有不同的能量和动量空间分布形式,其中声子散射信号表现出较强的色散行为,并且一般来说在散射强度上和 Q2 成正比。而纯晶场激发信号不具备色散特征,并且在散射强度上随 Q 值增加表现出和磁形状因子衰减一致的趋势。根据上述特点,我们可以对声子散射信号进行扣除,得到晶场激发信号。
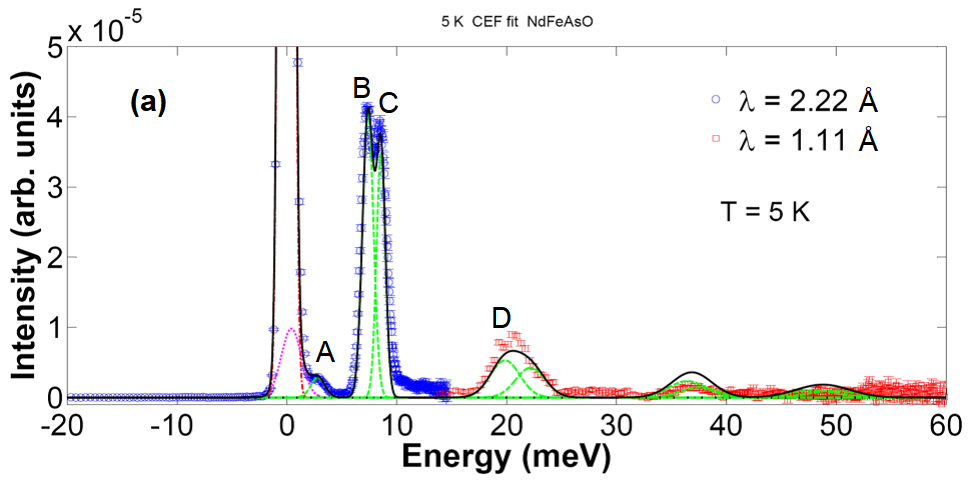
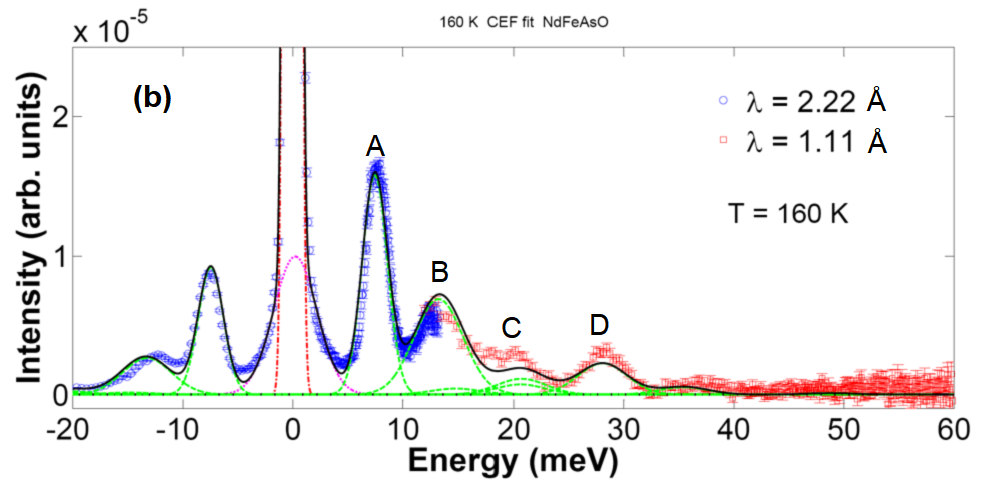
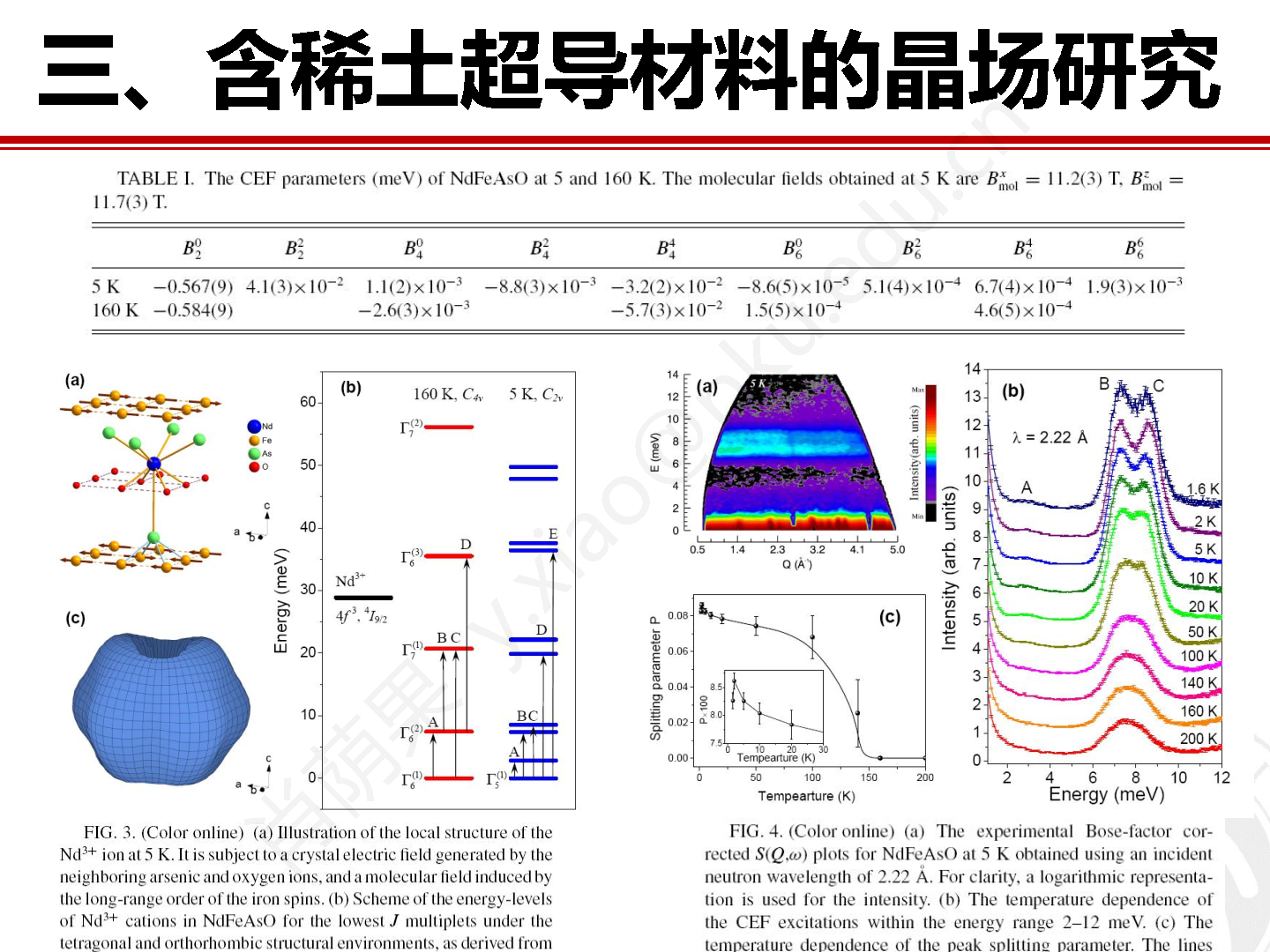
图13 稀土化合物 NdFeAsO 在 5 K 和 160 K 的晶场激发中子能谱实验和拟合数据。
图 13(a) 和 (b) 为校正之后 NdFeAsO 分别在 5 K 和 160 K 的晶场激发能谱。通过对比不同温度下非弹性峰的强度可以判断晶场激发是发生在基态和激发态之间还是在不同的激发态之间。随着温度降低,NdFeAsO 在 142 K 出现高温四方到低温正交的结构相变,并且在 137 K 时出现铁的自旋密度波磁相变。因此我们在分析 160 K 数据时只考虑晶场哈密顿量,而在分析 5 K数据时还需要额外考虑分子磁场的贡献:
![]()
高温四方相中,Nd3+ 位于具有 C4v 局域对称的 2c 晶位,晶场哈密顿量为:
![]()
十重简并态在晶场作用下劈裂为 3 个 Γ6 和 2 个 Γ7 克莱默二重态。
低温正交相中,Nd3+ 位于具有 C2v 局域对称的 4g 晶位,晶场哈密顿量为:
![]()
十重简并态在晶场作用下劈裂为 5 个 Γ5 克莱默二重态。如果只考虑晶场贡献,那么理论上在 5 K 的能谱上只能观察到 4 个激发峰,进一步的劈裂说明存在来自铁子晶格的分子磁场的贡献。在上述晶场模型下对数据进行拟合,就能得到表 3 中的晶场参数和分子场值以及图 14 中的晶场劈裂示意图。从图 14 中我们还可以看到 Nd3+ 中 4f 电子的空间电荷密度分布呈现非球形的各向异性特点,这也是导致体系出现磁晶各向异性的根本原因。
表3 稀土化合物 NdFeAsO 在 5 K 和 160 K 的晶场参数,此外分子场约为 11 T。

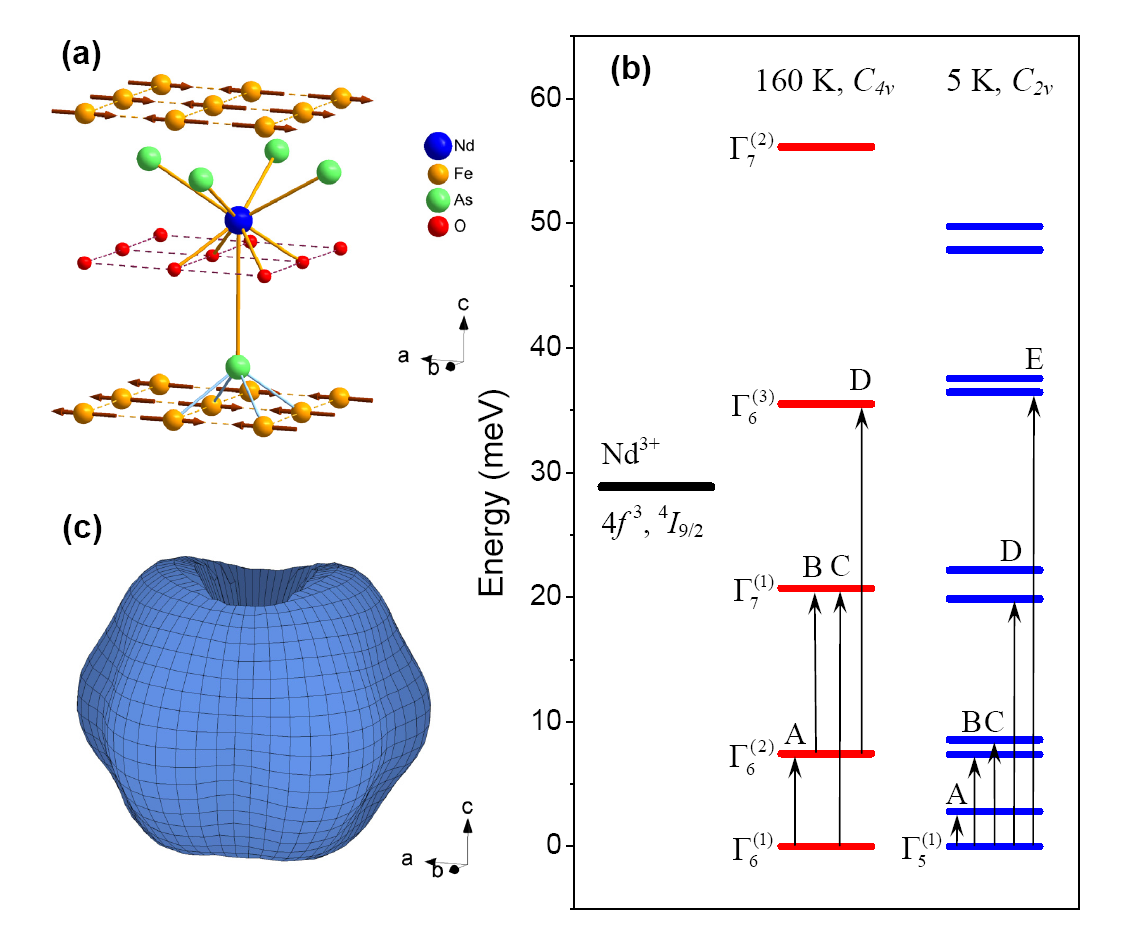
图14 稀土化合物 NdFeAsO 在 5 K 和 160 K 的晶场结构示意图。
前文中我们介绍了通过点电荷模型直接计算得到晶场参数的方法,但是该方法的前提是稀土离子只受到配位离子的静电势作用。而对于金属体系来说,传导电子会部分屏蔽配位离子静电势的作用,并且与 4f 电子发生相互作用,因此通过点电荷模型得到晶场参数的方法并不适用,而通过对非弹性中子散射实验数据直接进行分析得到的晶场参数更加准确可靠。除了晶场参数以外,可以看到 5 K 时作用于钕离子的铁分子场大约为 11 T,这也反映了 NdFeAsO 中稀土和过渡金属之间的耦合效应。
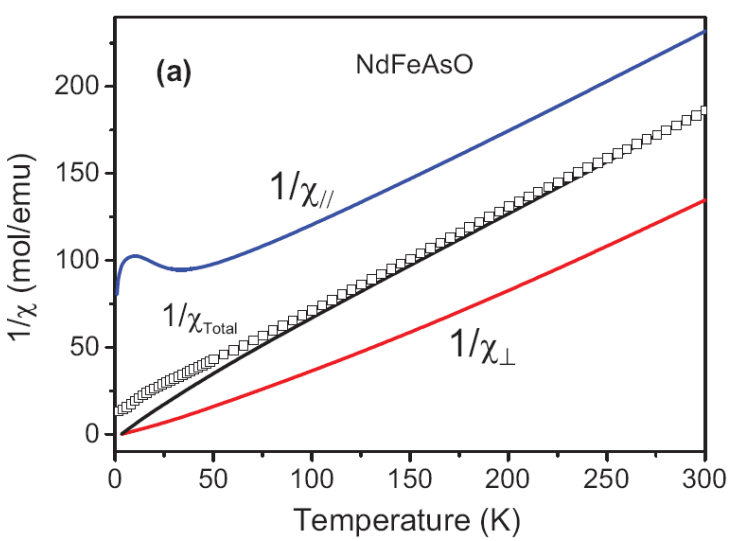
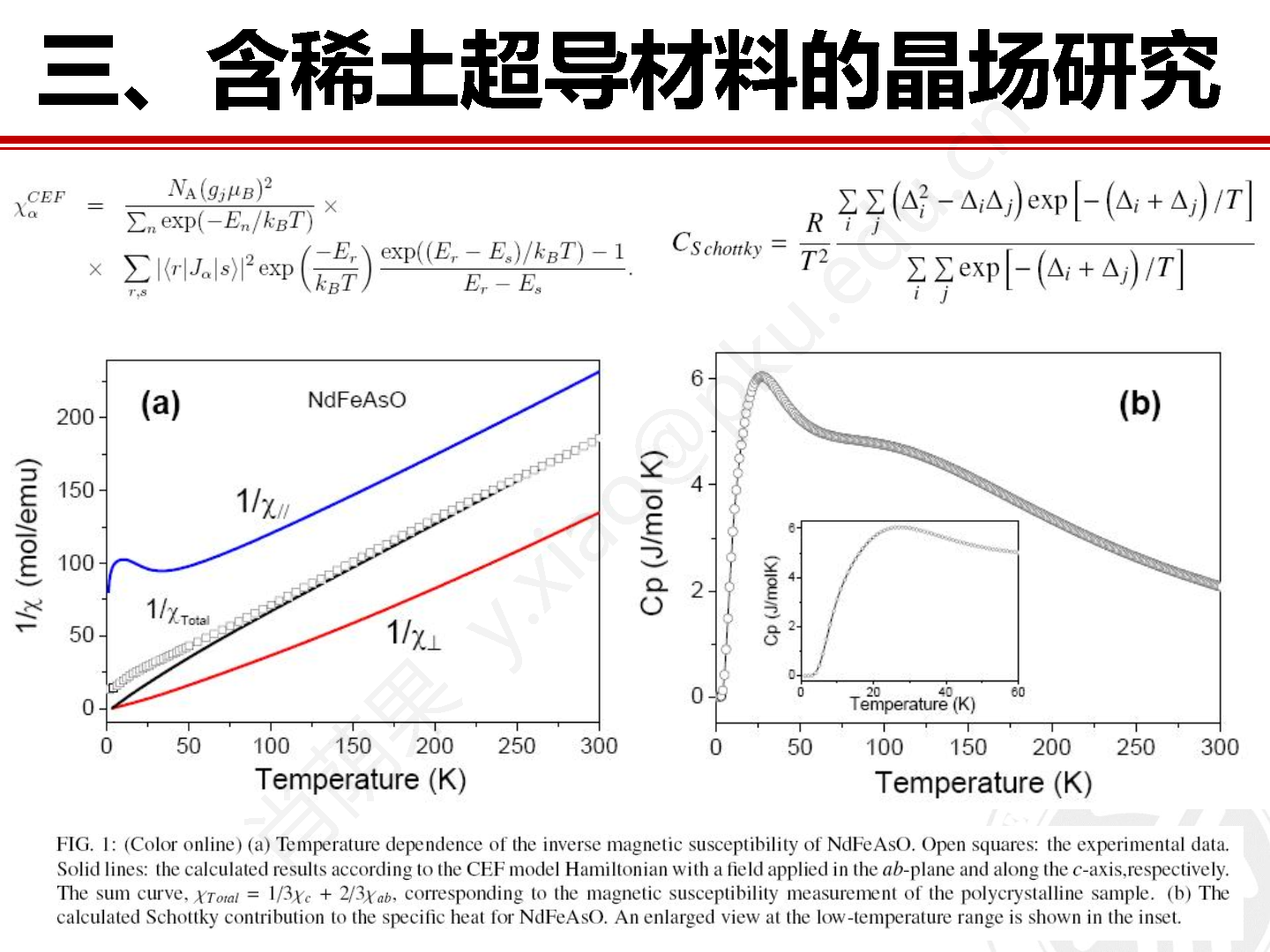
图15 根据晶场模型计算得到的 NdFeAsO 的磁化率和实验值对比。
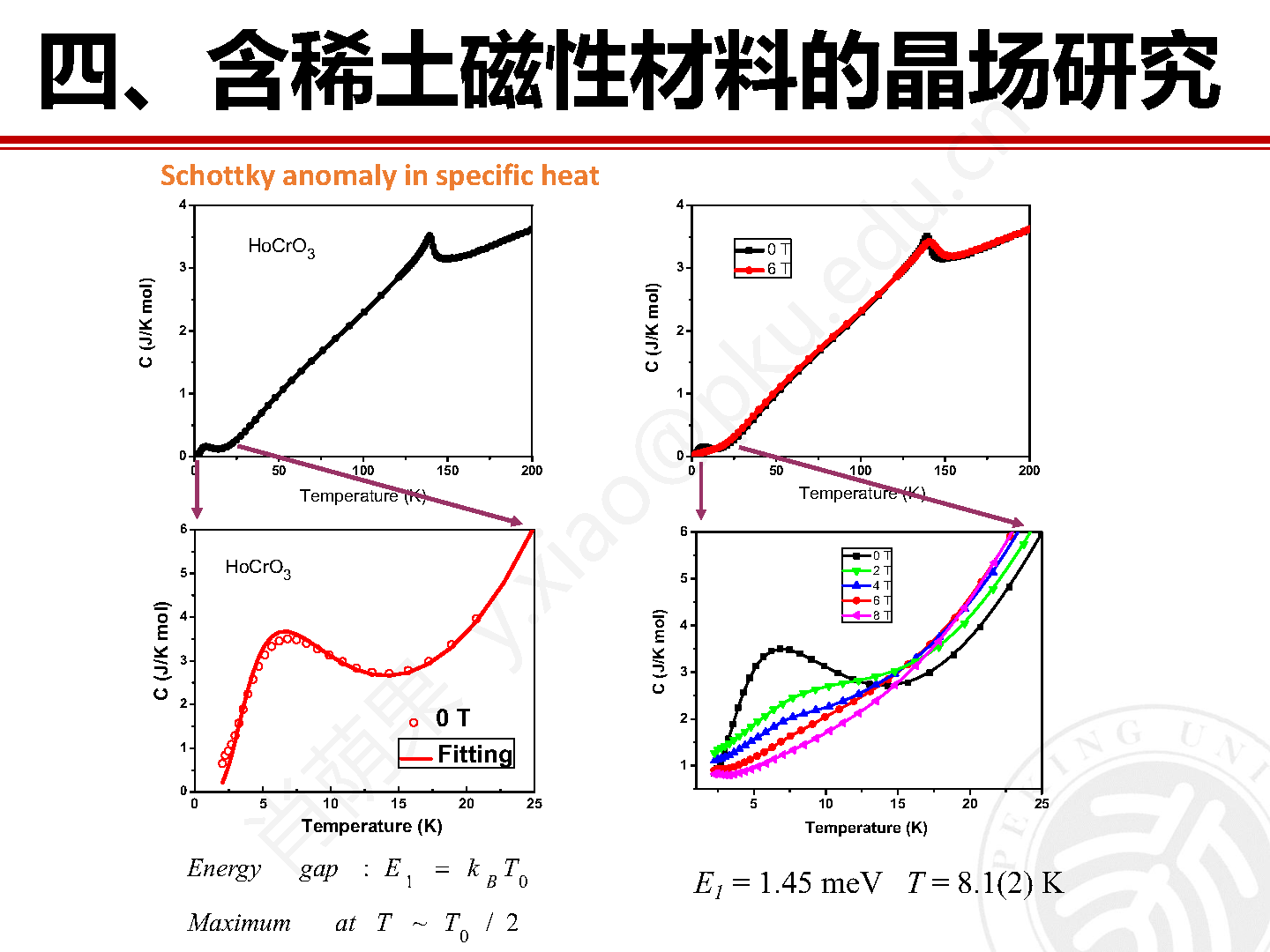
稀土材料体系的诸多宏观物性都与晶场效应密切相关。例如体系的磁化率可以用包含晶场哈密顿量矩阵元素的范弗莱克公式(Van Vleck formula)表达。根据前述拟合得到的 NdFeAsO 的晶场哈密顿量模型可以算得沿着 ab 平面和沿着 c 轴方向的磁化率,以及粉末平均的磁化率,如图 15 所示。可以看到实验测得的磁化率基本上可以很好地用晶场模型来解释,低温部分偏差较大主要是归因于铁磁子晶格的贡献。此外,体系比热的肖特基贡献部分也可以由晶场模型算得,该部分贡献一般会以低温区肖特基异常峰(Schottky anomaly)的形式出现。其它例如磁熵、电阻和热膨胀等重要宏观物性也可以由稀土晶场结构信息计算得到。
4. 总结
稀土具有优良的光电磁等物理特性,是能源材料和信息材料等高科技发展的重要战略资源。我国拥有丰富的稀土矿产资源,探明的储量居世界之首,为发展我国光电磁稀土功能材料产业提供了坚实的基础。在含有稀土元素的晶体材料中,围绕在稀土离子周围的晶格上的离子所产生的电场,即晶体场,能够将稀土离子的多重简并基态去简并化。而电子在不同轨道能级之间的跃迁会引起晶场激发现象。非弹性中子散射方法是探测稀土材料中晶场激发和不连续晶场结构的重要独特方法。首先通过中子散射实验得到完整的晶场能谱,通过局域对称性分析快速得到由晶场参数和史蒂芬等价算符构成的稀土离子的晶场哈密顿量,通过对晶场哈密顿量的解析可以对非弹性中子数据进行拟合,取得重要的能够反映稀土离子磁各向异性的稀土晶场结构信息。对稀土离子晶场激发的非弹性中子散射研究和计算模拟可以应用于对各类稀土功能材料的探索中。
由于强中子吸收的稀土元素占比较高,因此选取适当的稀土体系或采用同位素替代也是保证非弹性中子散射实验成功的关键。另外需要注意的是不同体系的晶场激发能量分布不同,从中子散射实验角度需要选取适当的入射中子能量以尽量获取所有晶场激发信号。晶场结构与稀土离子本身的总角动量和局域对称性密切相关,对于总角动量小局域对称性高的体系进行晶场分析相对较容易,而对于局域对称性低总角动量大的稀土离子,即使获取晶场激发谱也不能保证能够完成对其晶场能级的全面解析。此外,对于自旋轨道耦合作用较弱的 Sm3+ 和 Eu3+ 离子的晶场分析要注意区分多重简并基态和高阶多重态。同时还需要关注晶场激发与声子激发之间可能出现的强耦合作用,以及某些体系中可能出现的双离子相互作用引起的磁激发色散行为。总之,对稀土材料体系的晶场分析非常依赖于高质量中子散射实验数据的获取和可靠的微观模型的建立,在合理的物理模型框架下展开计算模拟才能真正有助于解释动力学物理表象,有助于通过对特定参数的优化实现对具有物理特性的稀土材料体系的筛选和探索。
参考文献
[1] M. T. Hutchings, in: Solid State Physics Vol. 16, ed. F. Seitz and D. Thurnbull, (Academic Press, New York and London, 1964).
[2] K. W. H. Stevens, Matrix Elements and Operator Equivalents Connected with the Magnetic Properties of Rare Earth Ions, Proc. Phys. Soc. A 65 (1952) 209.
[3] B. G. Wybourne, Spectroscopic Properties of Rare Earths, (Interscience, New York, 1965).
[4] R. Lea, M. J. M. Leask and W. P. Wolf, The Raising of Angular Momentum Degeneracy of f-electron Terms by Cubic Crystal Fields, J. Phys. Chem. Solids 23 (1962) 1381-1405.
[5] A. Furrer, Crystal Field Effects in Metals and Alloys, (New York: Plenum Press 1977).
[6] D. Newman and B. K. C. Ng, Crystal Field Handbook, (Cambridge University Press, 2000).
[7] E. Bauer, M. Rotter, Magnetism of Complex Metallic Alloys: Crystalline Electric Field Effects, (CMA Euroschool, Ljubljana, Slovenia 2007).
[8] E. Balcar and S. W. Lovesey, Theory of Magnetic Neutron and Photon Scattering, (Oxford University Press, 1989).
[9] B. Frick and M. Loewenhaupt, Crystal Field Spectroscopy by Inelastic Neutron Scattering, Z. Phys. B – Condensed Matter 63 (1986) 213-230.
[10] J. Jensen and A. R. Mackintosh, Rare Earth Magnetism, (Clarendon Press Oxford 1991).
[11] A. T. Boothroyd, Principles of Neutron Scattering from Condensed Matter, (Oxford University Press 2020).
[12] Y. Xiao, et al., Inelastic Neutron Scattering Study of Crystal Field Excitations of Nd3+ in NdFeAsO, Phys. Rev. B 88 (2013)214419.