四. 非弹性中子散射方法之自旋波激发
1. 前言
凝聚态物质是由大量粒子组成,并且粒子间存在较强相互作用的系统。物质的静态结构由系统的基态决定,而物质的动力学性质与其激发态相关联。前文中我们讨论了弹性中子散射方法研究凝聚态物质的晶体结构和磁结构,在此我们将讨论非弹性中子散射方法研究凝聚态物质的动力学特性。凝聚态物质的动力学特性通常表现为集体激发现象,并且与其热学性能和磁性能等物理性质直接相关,是深入理解结构相变和磁相变以及温度依赖现象的重要基础。物质的动力学特性可以通过对系统元激发的实验研究直接得到。非弹性中子散射方法是研究凝聚态物质中元激发,包括声子激发、自旋波激发和晶场激发等的重要实验方法。
在自旋晶格系统中,磁性离子自旋的有序排列状态就是系统的基态,比如常见的铁磁有序、反铁磁有序和亚铁磁有序基态。如果系统的基态受到微扰,例如某一个初始格点上的自旋偏离量子化轴的方向,那么系统将处于一个低能激发态。由于相邻自旋之间存在相互作用就会使临近初始格点的自旋取向也发生改变,并且继续影响次近邻格点自旋,最后以集体偏离轴向的运行形式扩散和传播。同时相邻自旋也会通过自旋间的相互作用试图使偏离量子化轴方向的初始格点上的自旋方向恢复轴向状态。最终在物质的晶格中会形成自旋的震荡,表现为自旋在格点上类似波动行为的进动。这种自旋的波动就是自旋波,自旋波的量子就是磁振子。磁振子和晶格振动对应的声子一样,都是凝聚态物质中的集体激发,并服从波色统计分布规律,因此也是一种玻色子。通过研究自旋波的色散关系,基于哈密顿量模型获得自旋相互作用系统的本征态,我们就能得到自旋之间的相互作用特性。
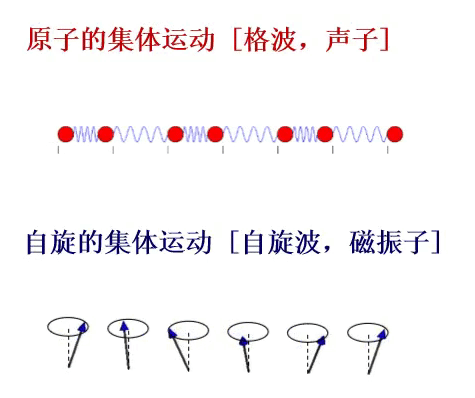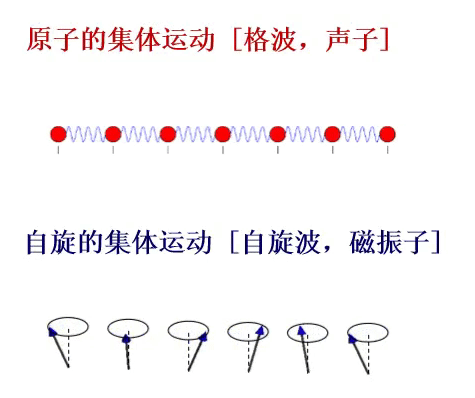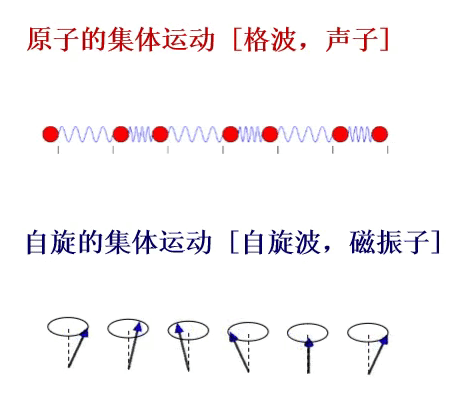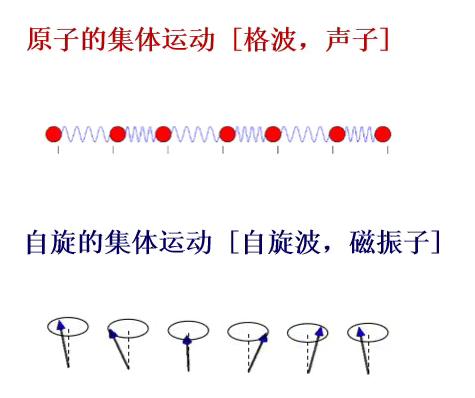
图1 凝聚态物质中的重要元激发:声子-格波的量子和磁振子-自旋波的量子。
研究自旋波激发的关键在于得到准确的色散关系,即ħω=f(q),也就是哈密顿量的本征值和激发的动量之间的关系。因此我们研究自旋波色散关系就必须应用能够与研究体系发生能量和动量交换的探针。虽然不同的磁性体系具有不同的磁转变温度,对应着不同的磁相互作用强度和磁激发能量,但是绝大多数磁性体系的磁激发能量一般在几个毫电子伏特(meV)到几百个毫电子伏特之间。而典型的冷中子和热中子的能量恰好能够覆盖几个meV到几百个meV的能量范围。 此外,凝聚态体系中动量与其原子间距相关,一般都落在几个Å-1的范围内,这也正是中子的可探测范围。加之中子磁偶极矩的存在,使中子与体系中原子磁矩之间产生相互作用,因此中子是研究磁激发的最有效的微探针。当中子射向凝聚态体系,并被体系散射之后后,通过建立动量转移和能量转移之间的关系,我们便可以从实验上得到体系的自旋波激发色散关系,并通过建立理论模型对其色散关系进行分析研究。
2. 非弹性中子散射方法
前文中我们已经讨论过,当中子在被体系散射的过程中不发生能量变化的过程为弹性散射,而非弹性散射过程必然伴随发生能量的转移。弹性中子散射过程中的入射矢量ki和出射矢量kf方向不同大小相等(图2)。而在非弹性中子散射过程中,能量在中子和体系之间发生转移,散射矢量关系也相应地发生变化(图3)。入射矢量和出射矢量与散射矢量以及能量之间的关系为:
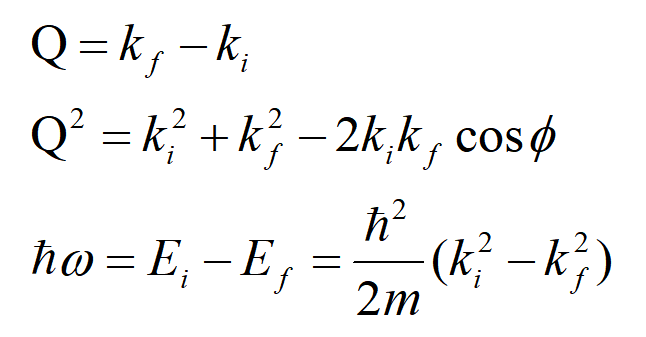
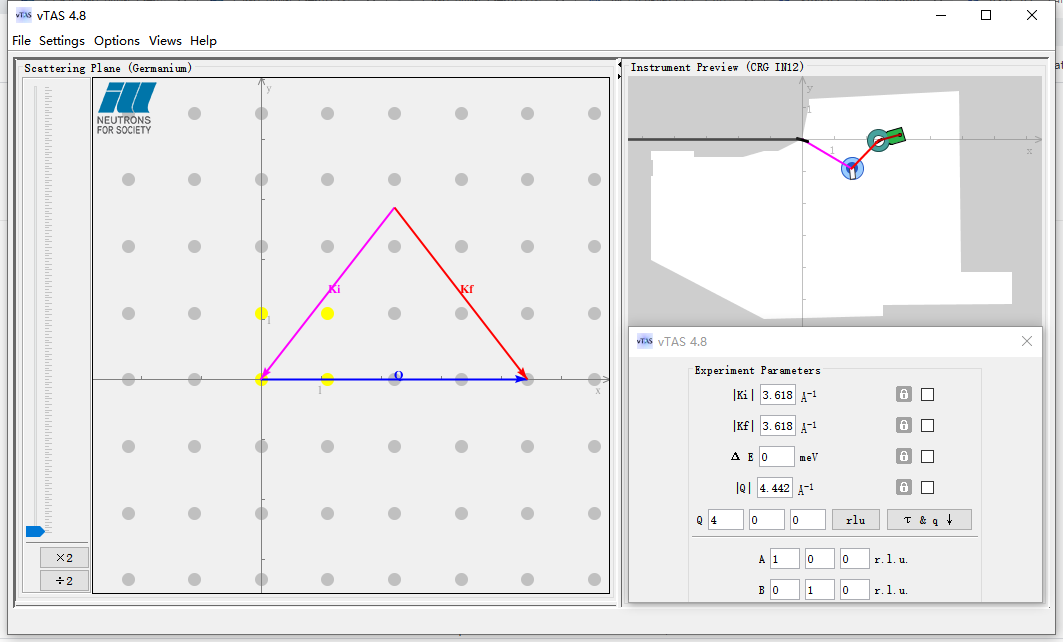
图2 对应于倒空间中锗(400)衍射峰的弹性散射过程的矢量关系(ki = kf)。
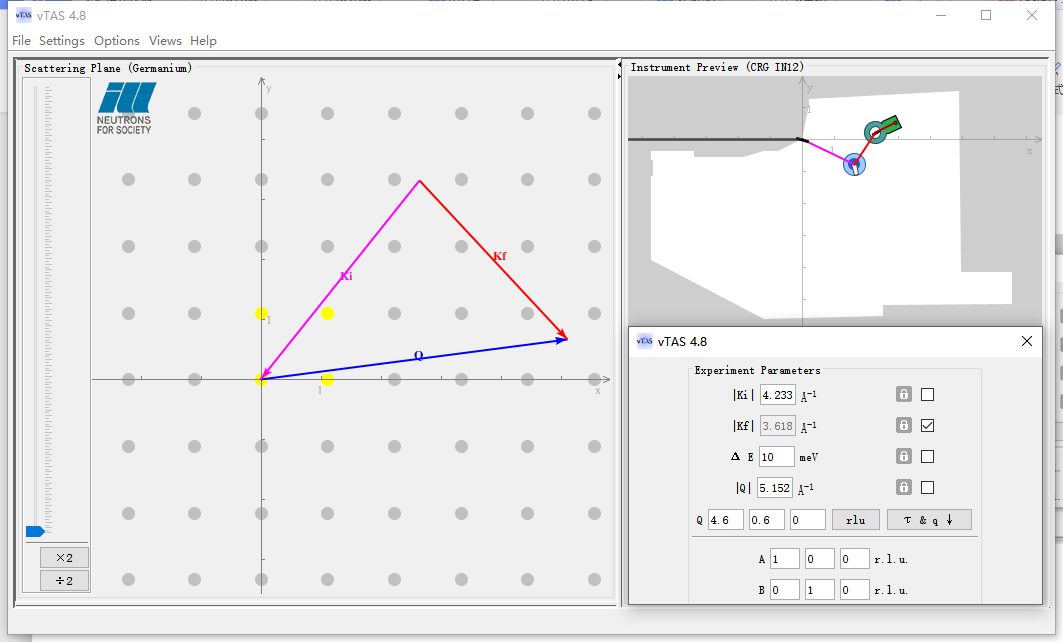
通过非弹性中子散射方法可测得的动量转移和能量转移范围与入射中子的能量密切相关,因此在仪器硬件不受限的条件下首先要保证入射矢量、出射矢量和散射矢量之间能够形成三角闭环,其次要保证在特定的布里渊区能够实现预期的能量转移。非弹性中子散射方法的应用,特别是在自旋波激发方面的应用主要可以通过三轴中子谱仪和飞行时间中子谱仪这两类谱仪装置得以实现。
2.1 三轴中子谱仪
三轴中子谱仪是最常用的研究自旋波激发的实验装置。三轴中子谱仪的发明人Bertram N. Brockhouse 因其在中子谱学发展中的重要贡献,和发展了中子衍射技术的Clifford G. Shull共同获得了1994年的诺贝尔物理学奖。顾名思义,中子三轴谱仪具有三个旋转轴,在三个旋转轴上分别放置三个重要部件,依次是单色器、样品和分析晶体。旋转单色器可以得到不同波长/能量的入射中子,旋转样品可以得到不同的散射角和入射中子波矢,旋转分析晶体可以得到不同波长/能量的散射中子。通过三个轴的联动旋转我们就能够得到在倒空间平面中各个位置的能量变化。在三轴谱仪的实际应用中,我们一般通过分析晶体固定出射中子的能量,通过改变动量转移或者能量转移来分别获得固定能量扫描和固定动量扫描实验结果。一般来说三轴中子谱仪都是依托能够提供稳定中子束流的反应堆中子源搭建,通过中子光学器件不但可以对中子的能量进行选择并可以有效地聚焦中子增加束流强度。由于三轴谱仪的散射几何清晰明确,因此一般相比飞行时间中子谱仪具有更好的空间和能量分辨率。

采用三轴中子谱仪在倒空间中的扫描一般都是线扫描(固定Q扫描或固定E扫描),如果想得到整个倒空间的激发信号就必须进行逐个线扫描然后整合在一起,这个测试过程非常耗时,因此人们也发展了多路器分析技术,通过增加分析晶体建立更多的分析通道,覆盖更大的测试区间,提高测试效率。在利用非弹性中子散射技术研究体系元激发的过程中,我们需要首先建立实空间和倒空间的转换关系并通过矩阵参数切换,通常非弹实验的测试范围还受到三轴谱仪的硬件和空间限制,通过vTAS模拟软件可以直观地展示三轴谱仪布局和相应测试区间的矢量关系,对于理解非弹性中子散射实验和进行实验设计非常有帮助。
根据入射中子的能量以及相应的能量探测范围,三轴中子谱仪一般可以分为冷三轴和热三轴。目前我国也已经依托研究反应堆建设了数台三轴中子谱仪,包括四川绵阳的中国绵阳研究堆(CMRR)的冷中子三轴谱仪“鲲鹏”;中国先进研究堆(CARR)的中德热中子三轴谱仪SV30(固定ki模式),中科院物理所依托中国先进研究堆(CARR)建设的热中子三轴谱仪“翠竹”,中国人民大学依托中国先进研究堆(CARR)建设的冷中子三轴极化谱仪“行知”以及中国人民大学依托中国先进研究堆(CARR)建设的冷中子广谱谱仪“博雅”。这些谱仪在凝聚态物质的动力学研究方面已经取得了许多优秀的科研成果。
三轴中子谱仪目前在技术方面已经发展地非常成熟,Gen Shirane等在Neutron Scattering with a Triple-Axis Spectrometer Basic Techniques这本书里对三轴谱仪的原理和应用做了非常详尽的描述,特别是对分辨率方程(resolution function)和伪峰(spurious peaks)方面的讲解是同时基于散射原理和实践经验的全面总结,因此是依托三轴谱仪完成非弹性中子散射实验的重要参考。具体内容可参考该书,本文中就不展开讨论了。
2.2 飞行时间中子谱仪
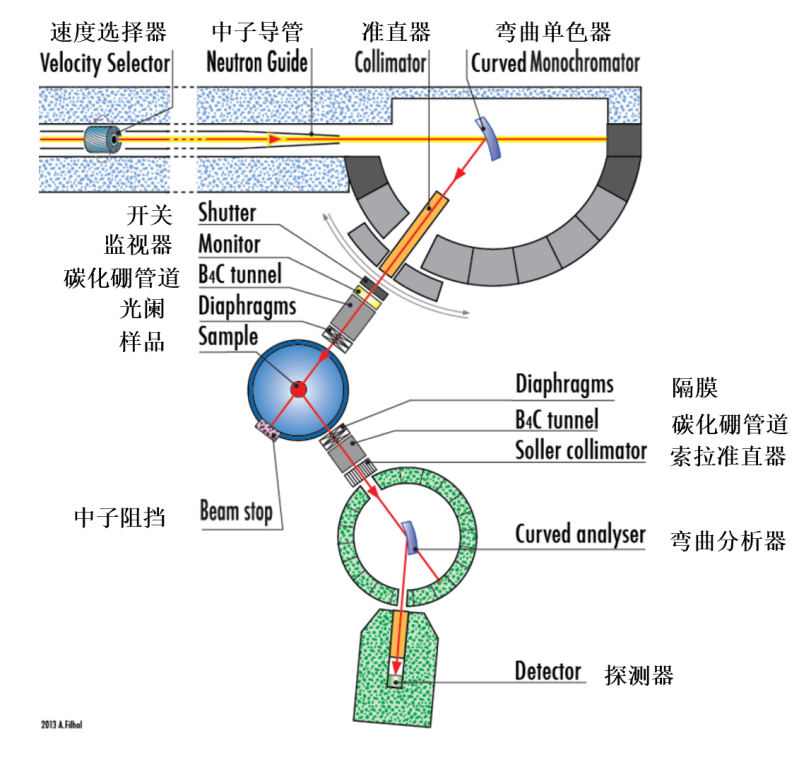
由于中子的能量和它的速度平方成正比,因此不同飞行速度的中子具有不同的能量。中子在被材料体系散射后,我们通过测量被样品散射的中子在样品和探测器之间已知的固定距离的飞行时间,就能够得到被散射中子的能量,从而判断中子和样品之间的能量交换,实现对非弹性中子散射的能量分析。然而采用飞行时间方法用到的中子脉冲都是微秒级别,在第一束中子到达探测器之后下一束中子脉冲才能开始飞行,因此这一方法更适用于脉冲式散裂中子源。虽然在反应堆式的稳态中子源也可以通过加装费米斩波器应用飞行时间中子谱仪,但是中子的利用效率较低,一般只有2%左右。飞行时间中子谱仪可以有两种设置,一种是直接几何,另一种是非直接几何,或者称为逆几何(图5)。在直接几何非弹谱仪中,入射中子首先通过斩波器被单色化,在和样品发生散射后又被不同散射角度的探测器探知。探测器记录散射中子的角度位置以及到达探测器的时间,并据此得到散射中子的波矢和能量。在非直接几何谱仪中,宽波段的中子射向样品,随后通过一系列分析晶体对散射中子的能量进行分析。虽然我国还没有可用的非弹性中子散射飞行时间谱仪,但是目前中山大学和散裂中子源科学中心正在依托中国散裂中子源联合建设高能直接几何非弹性中子散射飞行时间谱仪,该谱仪预计2022年底完成谱仪建设并面向用户开放。此外,依托中国散裂中子源的非直接几何谱仪非弹性中子谱仪也在规划建设中。
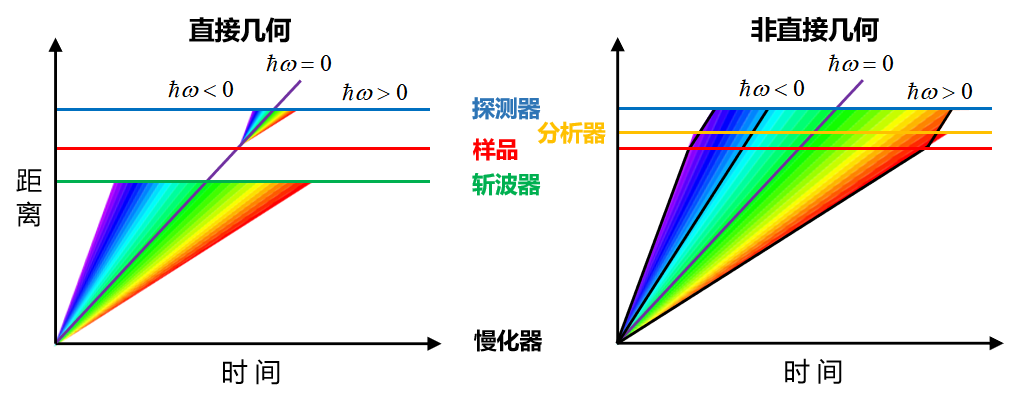
图5 直接几何和非直接几何非弹性中子散射飞行时间谱仪的中子飞行路径图。
3. 自旋波激发理论模型
具有自发磁矩的铁磁体中所有的自旋都平行排列,因此其磁晶胞和化学晶胞大小一致,并且交换常数大于零。通过铁磁自旋波理论可以对低能海森堡哈密顿量近似对角化得到自旋波解,其自旋波具有二次方色散特征(图6)。具有自旋反平行排列特征的反铁磁体的磁晶胞一般大于其化学晶胞,并且交换常数小于零。通过反铁磁自旋波理论结合双子晶格模型可以对低能海森堡哈密顿量近似对角化得到自旋波解,其自旋波具有线性色散特征(图6)。自旋波激发理论的详细推导可以很容易在固体物理或磁性物理教科书中找到,这里不再详述。

图6 铁磁体和反铁磁体的低温自旋波色散关系,D0为各向异性常数。
4. 自旋波激发研究实例
同时具有铁磁性和铁电性的多铁材料一直以来都是材料科学和凝聚态物理研究领域关注的热点,特别是具有较强磁电耦合的多铁材料更是蕴含了丰富的物理现象和物理内涵。MnWO4化合物是一种典型的自旋驱动铁电材料,因此深入研究该多铁材料的自旋动力学不但有助于理解其多铁特性并且有助于探索本征的磁电耦合机理。MnWO4为单斜P2/c结构,高自旋的Mn2+离子是晶胞中唯一的磁性离子,具有反铁磁的磁基态,传播矢量为k = (±1/4, 1/2, 1/2),磁结构如下图所示。

图7 MnWO4多铁化合物的低温晶体结构和反铁磁磁结构示意图。
通过MnWO4化合物13.5 K的磁转变温度可以判断其自旋波激发主要集中在低能量范围,因此可以选取冷中子非弹性中子散射谱仪对其自旋波激发进行研究。位于德国慕尼黑海因茨·迈尔-莱布尼茨中心(MLZ)反应堆,由德国于利希中子科学中心(JCNS)运行的冷中子三轴谱仪PANDA和位于美国橡树岭国家实验室(ORNL)散裂中子源(SNS)的冷中子飞行时间谱仪CNCS都是理想的选择。首先采用浮区单晶生长方法获得具有5克左右质量的大块单晶样品,并用劳厄衍射仪对单晶样品进行定向,使晶体的[102]和[010]方向保持在散射平面内,这样就能够通过非弹性中子实验获得磁布里渊区内沿着高对称方向的各点,如图8所示。 在采用冷中子三轴谱仪PANDA展开实验的过程中我们采用PG(002)单色器,同时在分析晶体前放置Be过滤器用于过滤高阶谐波中子。实验采用固定kf = 1.2 Å-1的模式,并有散射矢量 Q = (qx,qy,qz)Å-1, (HKL) = (qxa/2π,qyb/2π,qzc/2π)。图9是分别沿[102]和[010]方向测得的磁激发信号。

图8 MnWO4单晶及其定向示意图。

图9沿[102]和[010]方向的磁激发信号, (a)(c)实验数据(b)(d)理论计算。
通过线性自旋波近似可以对非弹性中子散射数据进行分析。首先,建立包含自旋交换部分和各向异性部分的海森堡哈密顿量:
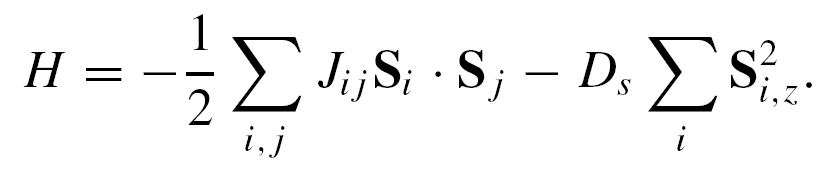
其中Jij代表图7中所示从J1到J12的自旋交换常数。Ds代表单轴单离子各向异性常数。MnWO4化合物共线反铁磁基态的磁单胞中总共有8个自旋,其中4个向上,4个向下。引入升降算符后可以对量子自旋进行线性的霍斯坦因-普里马科夫变换,有:

![]()
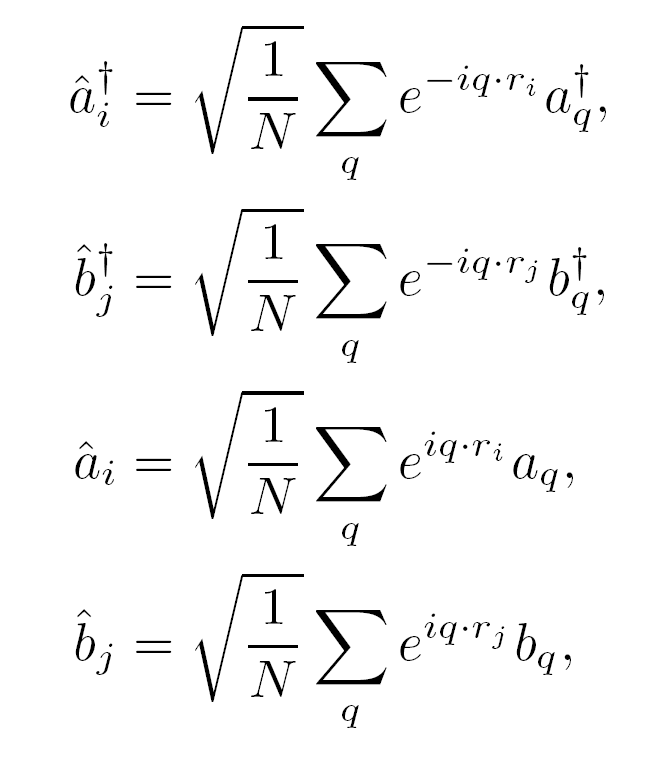
获得动量空间中的玻色哈密顿量为:
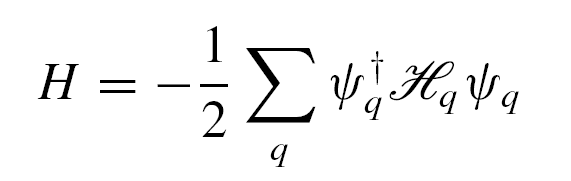


为了获得矩阵元素值需要对包含每个交换常数的项进行归纳整理,下面是对最近邻项J1以及其它几个交换常数的推导示例。
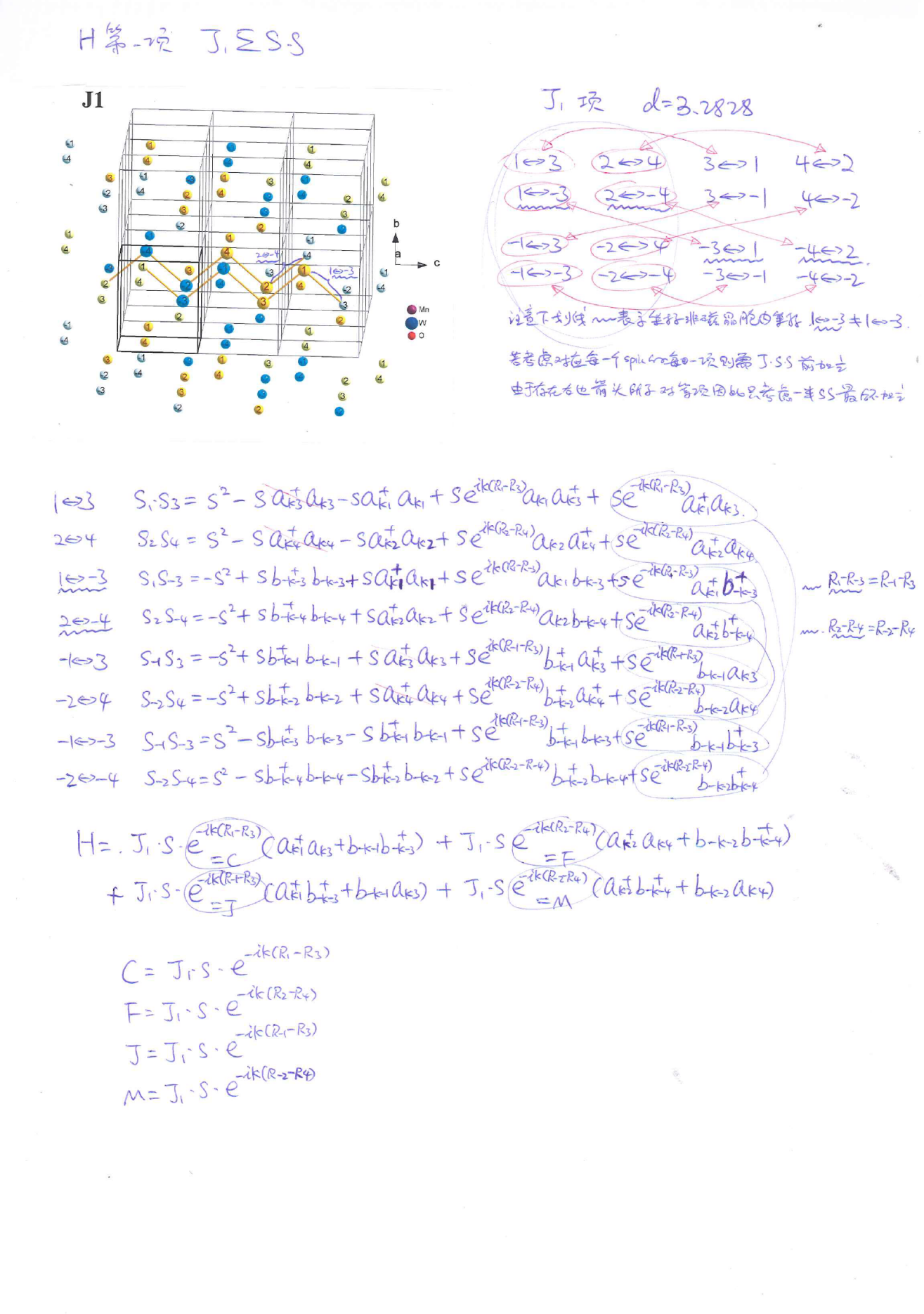



最后得到的矩阵元素为:

其中部分矩阵元素存在共轭关系,归纳整理后得到:
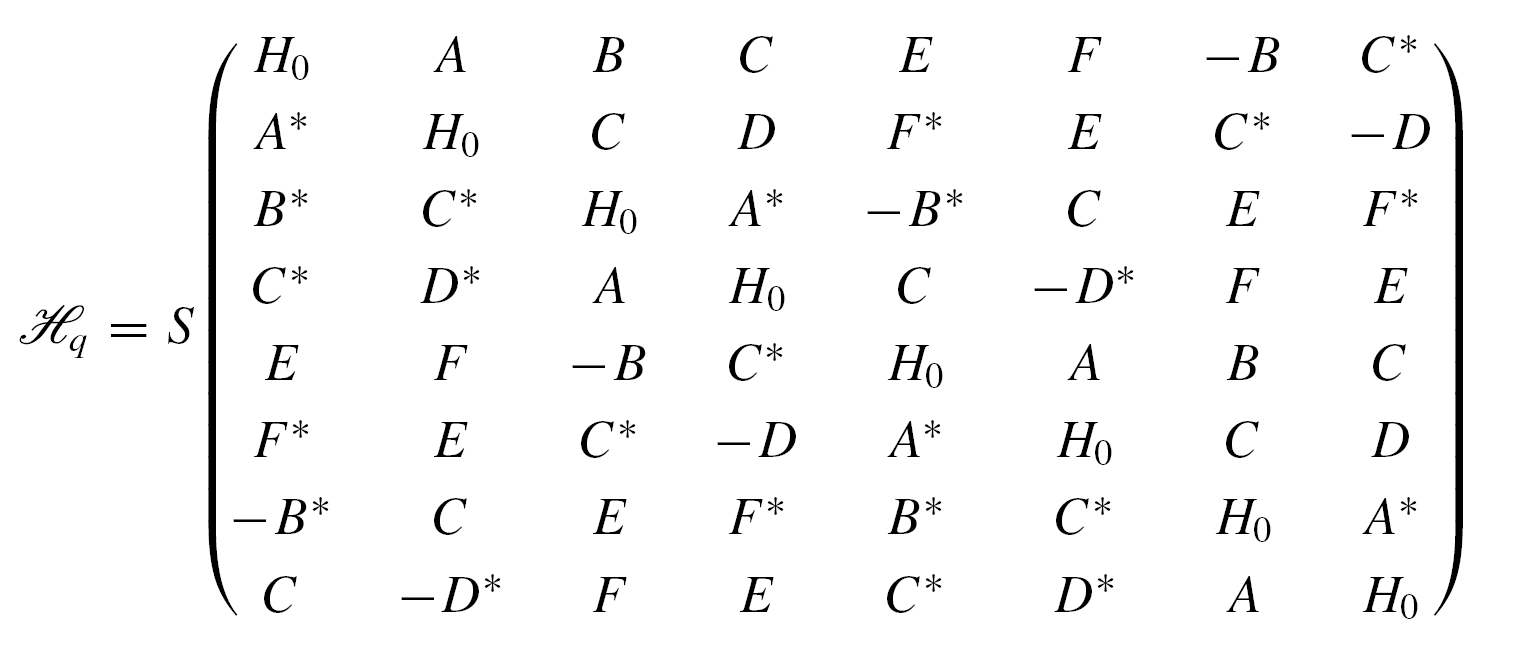
矩阵中包含各交换常数的矩阵元素为:

在取得玻色哈密顿量矩阵之后,不能直接用对角化厄米的方法对角化哈密顿量矩阵。需要借助不改变玻色对易关系的转换矩阵实现对角化,并得到实数本征值。这样就能够取得在倒空间中分别与自旋波量子数和自旋波态向量对应的本征值和本征矢量。这里我们用的是线性自旋波近似方法,而没有考虑自旋波之间的相互作用,如果把相互作用部分也加以考虑的话就需要解算符的非线性方程,在一维情况下该非线性方程有孤子解,代表非线性元激发。
结合非弹性中子散射截面就可以在线性自旋波理论模型的基础上对实验中子谱进行拟合。非弹性中子散射截面为:
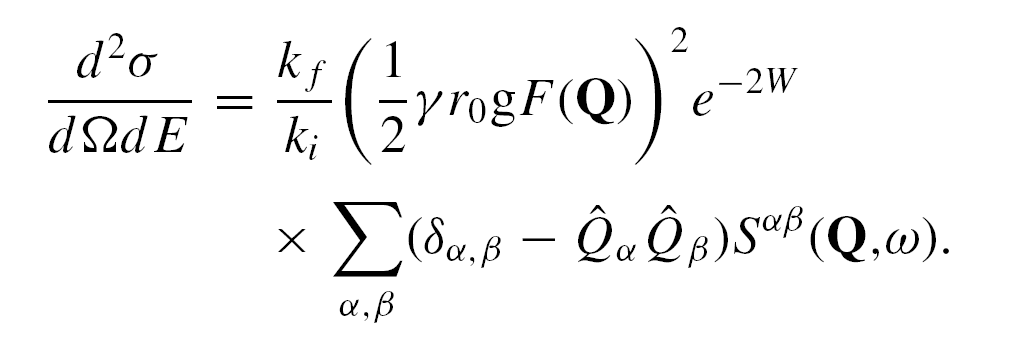
其中kf和ki分别为入射矢量和出射矢量,γr0 = 0.539×10-12 cm = 5.39 fm为单电子磁散射强度,g为朗德因子,F(Q)为Mn2+的磁形状因子,e-2W为德拜-沃勒因子,Sαβ(Q,ω)是自旋关联方程。 由于MnWO4的磁单胞中有8个Mn自旋,因此在零场下自旋波应该具有4支,每一支都是二重简并的。通过拟合交换常数我们可以得到和实验数据非常吻合的计算自旋波激发谱,如图9所示,相应地我们可以得到一系列代表自旋相互作用大小和性质的自旋交换常数。
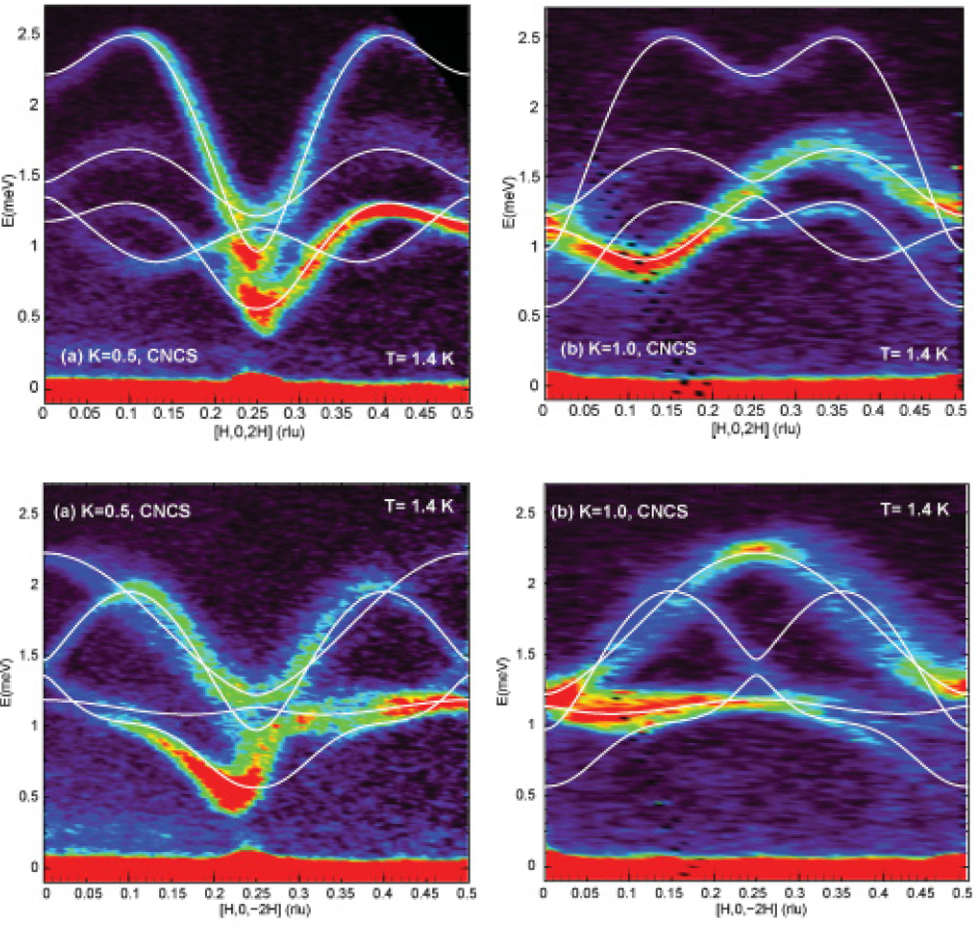
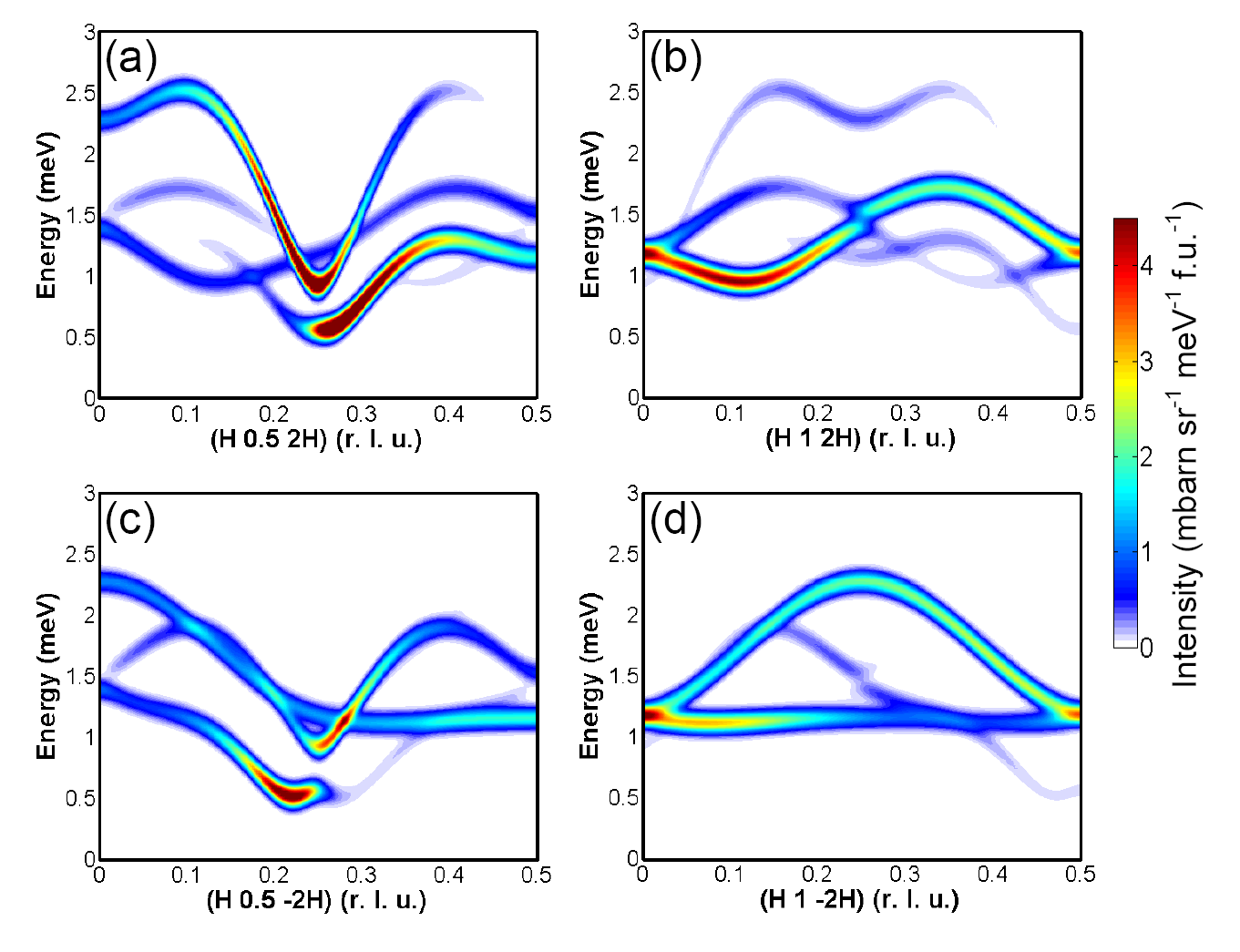
这些自旋波谱也可以通过配备费米斩波器的冷中子飞行时间谱仪获得(图10),入射中子的波长为 λ = 4.4 Å 。飞行时间中子谱仪的优势在于能够快速完成数据采集工作,通过单次测量就可以覆盖大面积Q-E空间,而三轴中子谱仪一次只能测得Q-E空间中的一点。由于具有出色的矩阵运算和可视化作图能力,MATLAB是分析自旋波激发中子数据的优秀软件之一。附件附上了MATLAB自旋波计算代码供参考。采用拟合得到的交换常数我们可以计算得到布里渊区中各个方向的自旋波色散关系或者各个能量的自旋波分布情况,例如与实验自旋波谱对应的沿着 [1 0 2]和[1 0 −2]方向的自旋波谱(图11),或者任意几个切面的色散关系(图12)。
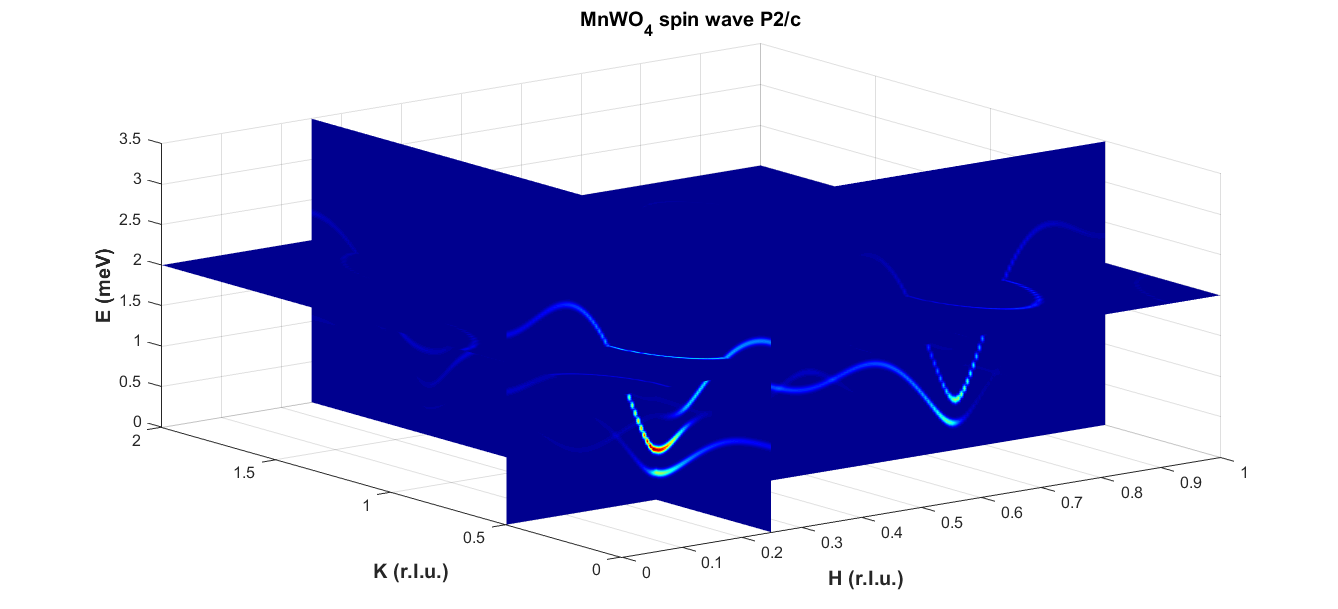
图12 MnWO4在布里渊区任意面上的自旋波激发谱。
自旋波是磁有序系统中常见的激发模式,可以用经典的海森堡模型进行描述。然而一些复杂磁系统中的相互作用或耦合会导致不能被海森堡模型所描述的复杂的磁激发行为出现,比如动态磁电耦合会导致新的集体激发现象出现,磁性三角晶格中几何阻搓引起的多重简并态磁激发等,这些都是引起广泛关注并值得深入研究的课题。
参考文献:
[1] T. Chatterji (Editor), Neutron Scattering from Magnetic Materials (2006) Elsevier.
[2] Th. Brückel et al., Neutron Scattering(2008), Forschungszentrum Jülich, Jülich.
[3] G. Shirane, S. M. Shapiro, and J. M. Tranquada, Neutron Scatteringwith a Triple-Axis SpectrometerBasic Techniques(2004) Cambridge University Press.
[4] M. Boehm, et al., Nuclear Inst. and Methods in Physics Research, A (2013) 697, 40-44.
[5] F. Ye, et al., Phys. Rev.B 83, 140401(R) (2011).
[6] Y. Xiao, et al., Phys. Rev.B 93, 214428 (2016).
[7] B.-Q. Liu, et al., J. Phys.: Condens. Matter 30, 295401 (2018).
[8] J. Wang, et al., Phys. Rev.B 98, 214425 (2018).