七．中子全散射和原子对分布函数
1. 引言
众所周知，通过布拉格衍射方法可以获取材料中原子排布的长程有序周期结构，然而布拉格衍射方法无法准确解析材料中存在的短程有序结构特征。对于目前快速发展的功能材料和纳米材料而言，原子尺度的短程有序局域结构与纳米结构特征常常决定了这些材料的关键性能。因此，侧重于周期性边界条件和长程有序的平移对称结构的传统晶体学分析方法已无法满足对该类材料结构精确解析的需求。一些具有元素分辨和空间分辨能力的谱学方法，如扩展X射线吸收精细结构（EXAFS）可以用于分析局域配位结构，但其定量分析材料整体结构特征的能力有限。中子或X射线全散射（Neutron/X-ray Total Scattering）技术能够同时采集样品的长程有序布拉格衍射峰以及材料中由于静态局域结构以及原子运动产生的弹性及非弹性漫散射信号，通过这种方式克服上述局限，全面深入地表征短程和局域有序结构[1–3]。基于全散射数据转化得到的原子对分布函数（Pair Distribution Function, PDF），作为一种实空间结构分析方法，能同时提供局域结构与长程结构特征信息，是研究晶态到非晶态凝聚态物质结构的重要方法。
2. 局域结构和全散射
在晶体材料中，原子核及核外电子云以三维周期性排列，并因此在散射图像中产生明确的相长干涉，即我们所熟知的布拉格衍射。通过对满足布拉格定律的衍射峰进行标定分析便可以得到材料长程有序结构，并用以确定晶体平均结构信息。然而实际晶体材料的结构本身非常复杂，原子结构并非完美的三维周期性排列，如图1所示。特别是由于结构缺陷和无序态普遍存在，原子偏离其固有位点。同时随着新型功能材料的发展，多样化的局域结构往往是决定材料优异性能的关键原因[4–6]，且局域结构包含原子对间距、配位数以及无序度等重要信息。对于具有特殊短程结构的材料，如纳米材料或非晶材料，其主要的结构信息也包含于局域结构之中。这类信息往往是衍射信号所忽略的，但其重要性不言而喻。
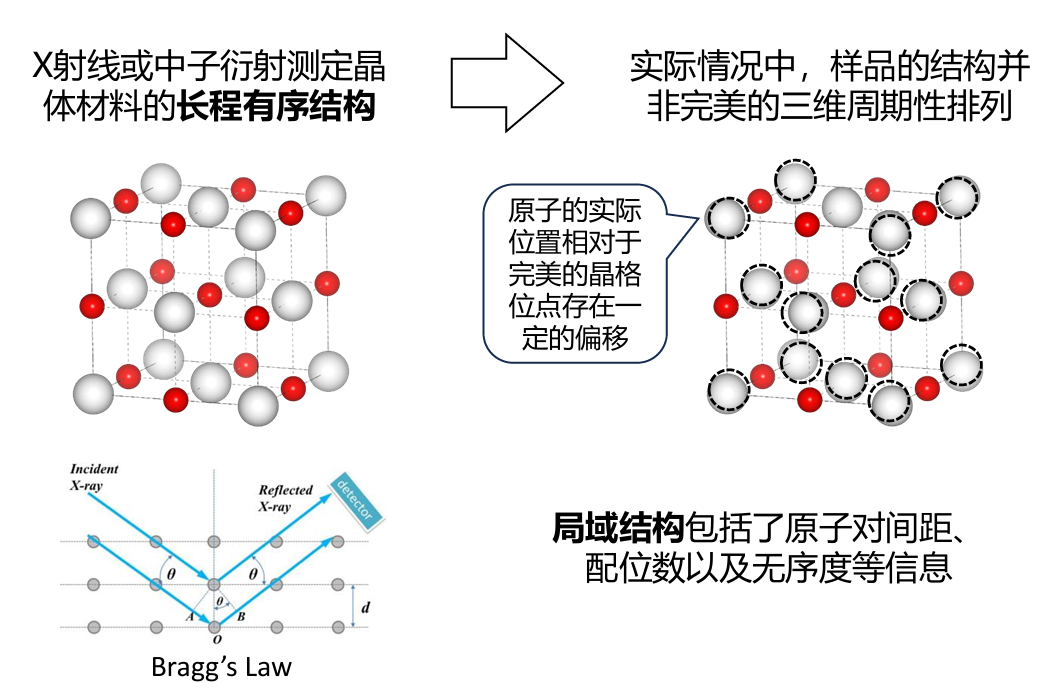
图 1 理想晶体与实际晶体局域结构差异
如前所述，任何原子排列都会使出射束产生干涉效应，形成对应的散射图像，但相对无规则的原子排列所产生的干涉效应，我们可以称之为漫散射，因其相对于布拉格衍射信号较微弱，往往隐藏于背底信号之中，如图2所示。如果我们能较好的收集并提取分析这部分漫散射信息，便同样可以获得关于局域结构中原子排列的信息。
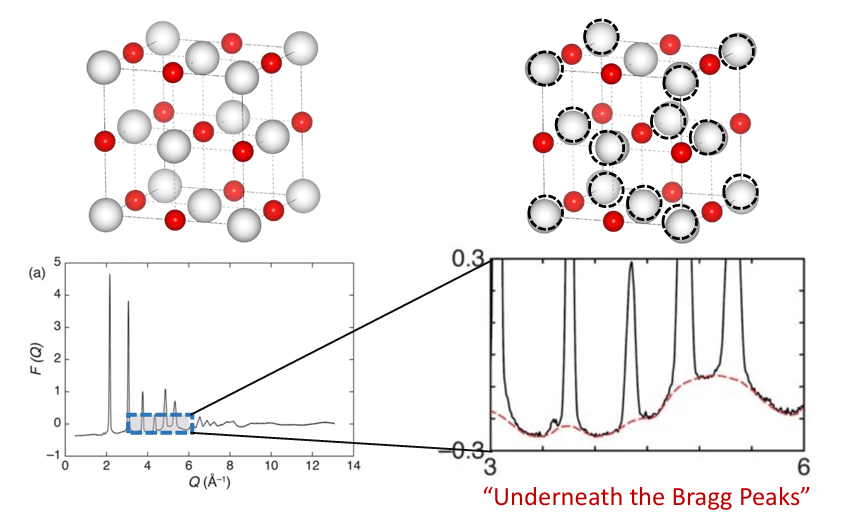
图 2 布拉格衍射与漫散射图像
材料总的散射信号由包含晶体长程结构信息的布拉格衍射和包含局域结构信息的漫散射组成，因此也可将其称为全散射信号。对于一个在位置 r → j 包含N个原子的结构，其全散射波矢量Q的振幅可以表示如下：
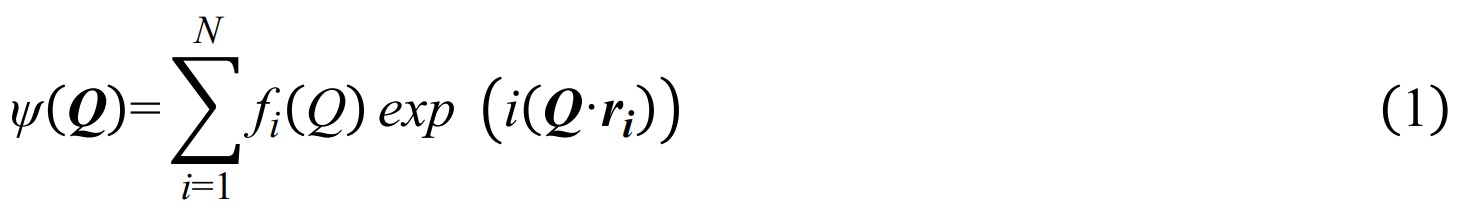
其中f i (Q)是原子的形状因子，在中子散射中它取决于对应原子的中子散射截面大小，在X射线散射中它取决于对应原子的电子数量和周围电子云密度。全散射波矢Q的公式对于晶体材料、非晶材料、纳米材料是完全通用的，例如对于理想的晶体材料，其全散射振幅仅在对应于布拉格峰位处非零，布拉格衍射振幅可表示为：
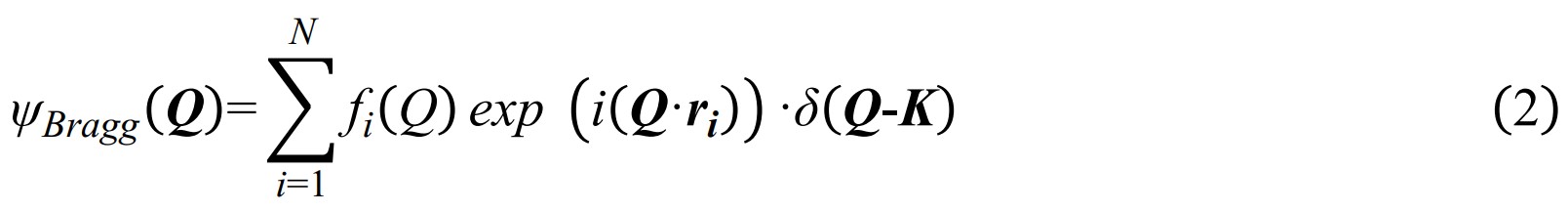
考虑到原子偏离理想位置的微小位移（u）与局域结构缺陷的贡献，漫散射振幅可以表示为：
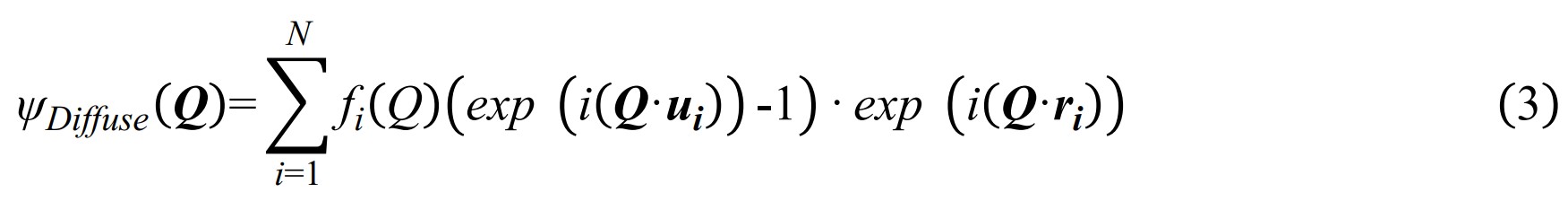
综上，我们已知全散射振幅是布拉格衍射与漫散射的线性叠加，通过数学工具也能非常直观的表达：
在实际的散射实验中往往采集的数据是与散射振幅的平方成正比的散射强度，我们同样可以用数学公式进行描述。通过将原子视为各向同性，散射振幅视为仅与Q相关的函数进行简化，可以得到散射方程：
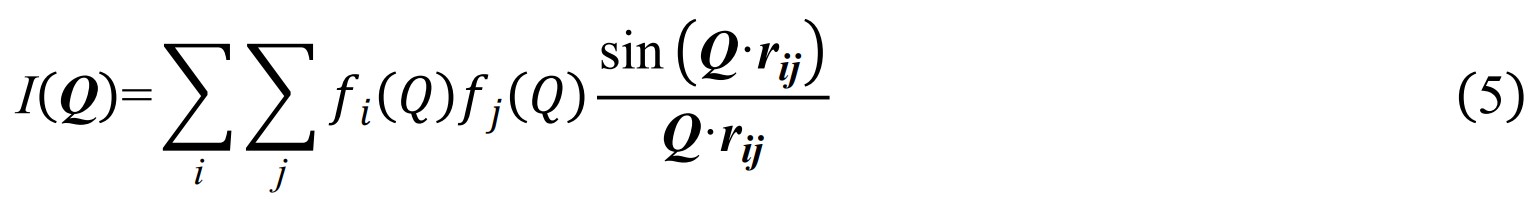
不难发现采集散射强度的过程中我们丢失了关于干涉波的绝对相位信息，即晶体学中的相位问题。这意味着我们能相对容易的实现ρ(r)或ri → I(Q)（从给定粒子位置r1，r2，···，rN）或电子密度分布ρ(r)，预测散射图案I(Q)但对于逆问题I(Q)→ ρ(r)或ri（从给定散射图案I(Q)，求解粒子位置r1，r2，···，rN或电子密度分布ρ(r)）的解决较为困难。对于晶体材料，特别是在单晶衍射中，已经开发了许多方法来克服这个问题，例如Rietveld方法通过不断迭代修改ri等参数直到理论计算的I(Q) 与实验观察到的I(Q)匹配，以此进行结构求解。[7] 但对于前文提到的局域无序或纳米/非晶材料，I(Q)的分析方法难以解析局域结构信息，因此我们需要引入全新的PDF方法[8]。
3. 对分布函数（PDF）
对分布函数（PDF）是一个大的函数家族，其中不同的函数之间由于定义和单位上的不同存在些许差异，但函数本身包含的信息非常类似，即用以描述样本数据中原子间距离的直方图，对分布函数g (r) 定义如下：
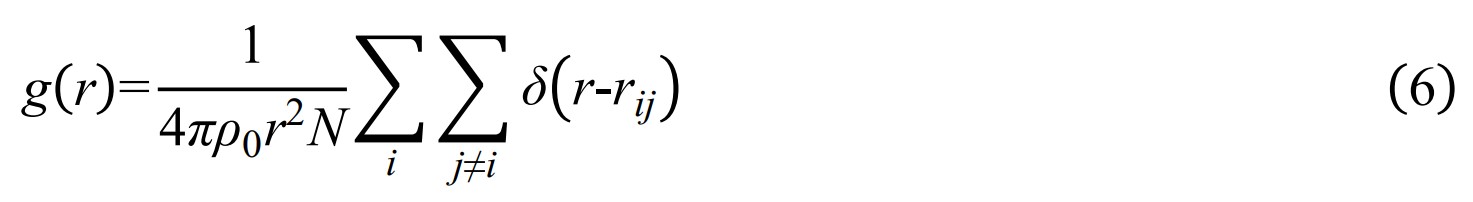
其中ρ0代表原子平均数量密度，N为原子总数，rij表示原子i和原子j之间的距离。δ (r−rij) 为Dirac-delta函数。直观上它反映了在一定距离r上找到相应原子对的概率[2,9]。
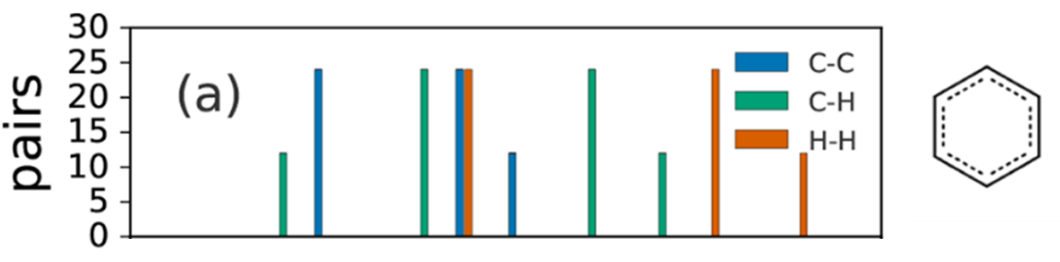
图 3 苯分子中原子对距离直方图 [3]
如图4为PDF家族中最典型的径向分布函数R(r)：
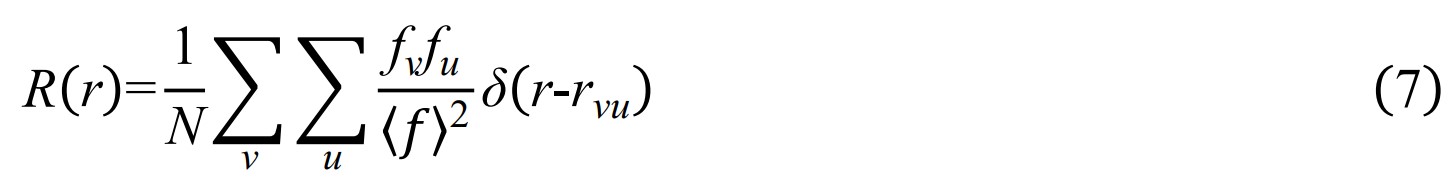
其中rvu是样品中第v个和第u个原子之间的距离，fu和fv是元素的形状因子。径向分布函数直观图像如下所示，表示以某一原子为中心的半径为r，厚度为 dr 的球壳内包含的原子数。RDF峰位置直接给出了样品中原子之间的距离，它们的强度取决于原子对的形状因子（fu和fv依赖性），以及给定距离的原子对数目。
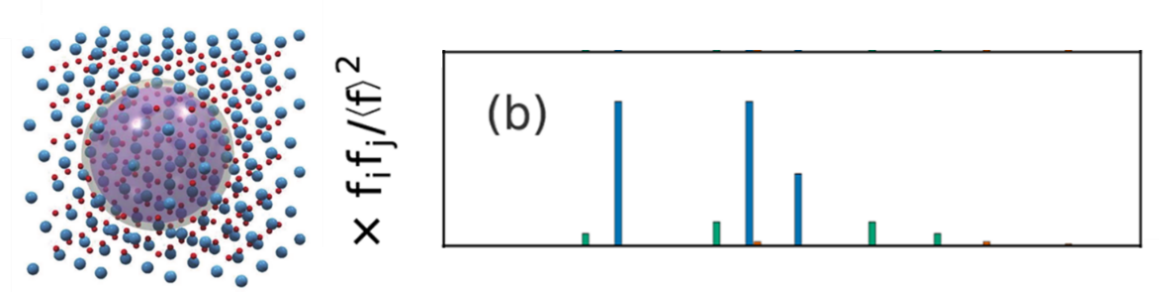
图 4 引入原子散射功率加权后苯分子中原子对的径向分布函数图像 [3]
在此基础上进一步卷积上原子热运动、仪器参数等导致峰形宽化因素的影响，我们便可以得到单个苯分子的模拟RDFs图像（图5）。
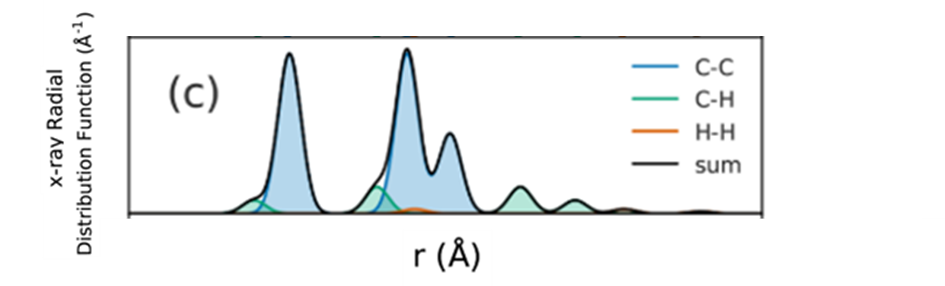
图 5 单个苯分子模拟RDFs图像 [3]
而在全散射分析中常用到的PDF函数是G(r)，G(r)和R(r)之间的关系由下式给出：
其中ρ0是原子密度，即样品单位体积中的原子数。虽然 R(r) 比 G(r) 更为直观，但我们在做PDF分析时更多的使用G(r) 。这有几个原因，最重要的是G(r) 是我们直接从处理后的实验数据的傅里叶变换中得到的函数。如果要计算R(r) 或任何其他相关的PDF函数，需要对样品结构做出假设，如原子序数、原子密度和颗粒大小及形状，而这些信息不一定已知。随着r的增加，R(r) 作为与r2正相关的函数会随之发散。如果分析原点原子周围某个固定距离处的近邻原子数量，我们会意识到随着r的增加，原子的数量会越来越多，因为在r处球体的尺寸变得越来越大。从实用的角度来看，这使得R(r) 函数的可视化非常不方便。相反，如图6所示，G(r)在零点附近振荡，并且PDF峰的振幅给出了样品中结构相干性的直接信息。如果样本具有完全随机分布，G(r)将是一条平坦的线。如果某个原子间距离出现频率较高，即大于平均值，则能够在G(r)中看到正峰，而小于平均值的原子间距离将给出负值，注意在中子PDF中峰值的正负还取决于原子对中两原子的中子散射因子乘积的正负取值。最后，在G(r)函数中，实验的不确定性在r范围内近似恒定，这也能得到更可靠的PDF建模和数据的可视化解释。
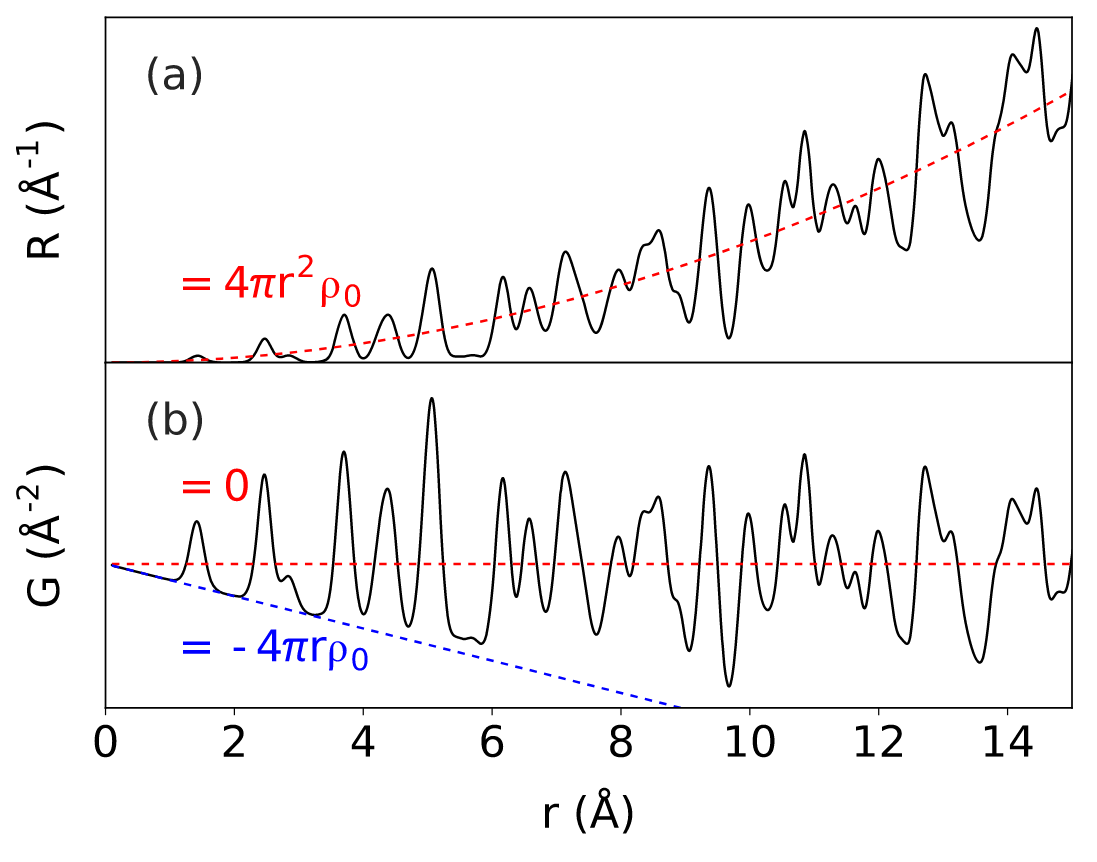
图 6 RDF和归一化的PDF图像:(a) RDF (黑色) 红色代表渐近；(b)相应PDF (黑色) 红色表示渐近，蓝色表示负倾斜基线 [3]
因此，PDF作为一种简单的一维函数，其包含材料中结构相关性的信息。PDF 的优势在于PDF相关信息包含于全散射信息并容易通过实验测量得到，其次，在运用PDF分析时如果从已知结构进行计算十分简便。同时该分析方法提供了一种非常直观的局域结构视图。严格来说，它是直接从原子密度的自相关函数推导而来。但直观上它反映了在一定距离r上找到相应原子对的概率。
4. 通过全散射数据获取PDF
如前所述，总散射是由各个原子对于X射线或中子束单独的散射通过干涉效应组成，散射矢量Q对应倒易空间中的“频率”，而原子间距r对应实空间中的“位置”。傅里叶变换天然地连接了这两个空间，因此我们可以通过对测量的散射强度进行傅里叶变换，将全散射信号转换为与中子/X射线散射的原子/电子位置相关的峰形函数，即对分布函数（PDF）。但直接对I(Q)进行傅里叶变换会引入原子形状因子等非结构因素的卷积，导致结果偏离真实原子分布。因此，我们需要先对全散射信号进行归一化处理以获得全散射结构函数：
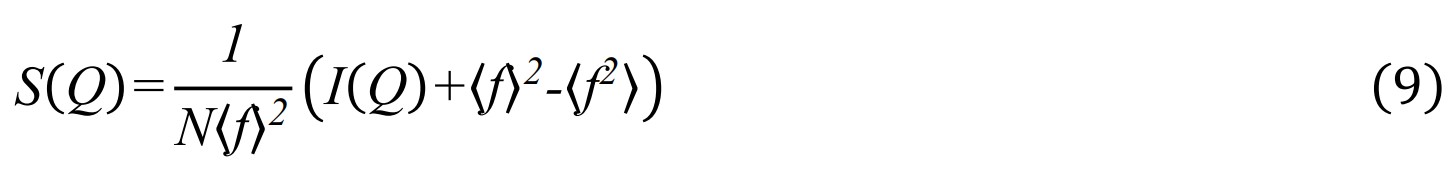
S(Q) 通过散射强度除以散射体的数量N和每个原子的平均散射功率进行归一，平均散射功率由原子平均形状因子的平方项给出。同时通过可以消除单个散射体形状因子的方差影响，保留与位置关联相关的结构信息。
在此基础上我们需要对全散射结构函数进行进一步约化，得到傅里叶变换的核函数：
由于S(Q)的定义中仍包含平均密度项ρ0，故需要通过S(Q)–1扣除平均密度的影响。同时考虑到S(Q)在高Q区域的信号强度会因原子形状因子随散射角度增大而显著衰减，通过乘以Q，可放大高Q区域的微弱振荡信号，从而在傅里叶变换后提升G(r) 的分辨率。现在可以对F(Q)进行正弦傅里叶变换，从而得到约化的对分布函数：
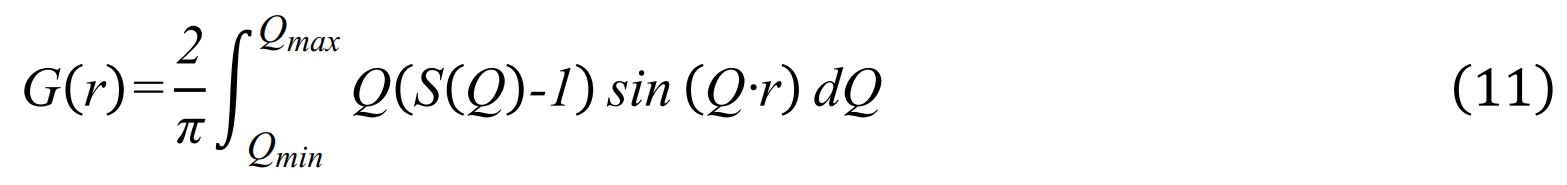
PDF函数图像能直观的为我们提供材料局域结构的相关信息，例如峰位表示实空间中原子对键长；峰宽表示原子的热振动及无序度或键长畸变；峰强表示原子配位数/占有率；峰衰减表示材料的尺寸形貌。具体的PDF分析方法我们将在之后的部分介绍。
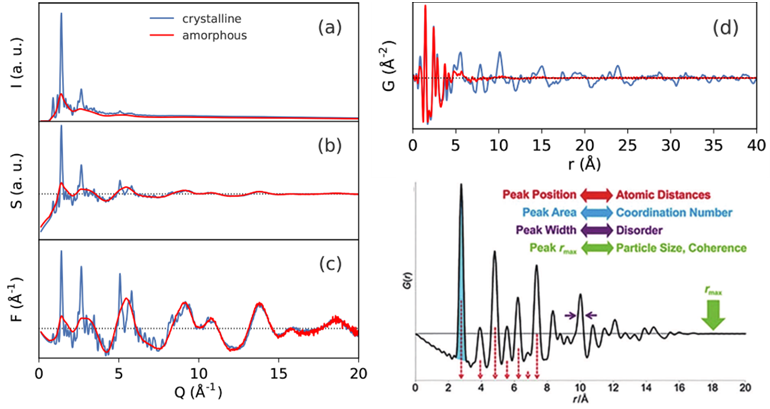
图 7 PDF函数规约转化过程及所包含的直观信息
5. 全散射数据的实验和分析
常见的全散射数据采集通过利用准直高能束流透射穿过样品并测量。全散射意味着布拉格衍射强度和漫散射强度都被有效收集。其中最重要的一点是确保能在足够宽的Q范围（较大的Qmax）内获取数据，以便尽可能多的包含倒空间信息，确保PDF中的原子对距离在傅里叶变换后可以被准确分辨。最为常见也最为迅速的全散射数据采集通常在世界各地的同步辐射加速器上的高能X射线，通常能量为40-90 keV的光束线上进行，就数据质量而言，同步辐射高能X射线相较于实验室线源能实现极高的光子通量，从而大大缩短采样时间。同时高能X射线能更好的穿透样品，实现对重元素或较厚样品的数据采集，或从复杂环境中进行样品数据采集。但随着实验室设备的技术发展，目前X射线全散射数据也能从实验室x射线粉末衍射仪获得，但与同步辐射线源分钟级的测试速率不同，这类数据采集通常需要15-30小时以获得足够的光子通量。同时为覆盖足够的高Q值范围，我们需要更换谱仪靶材以实现较小波长的X射线。常见的铜靶难以满足需求，而银靶可以实现与同步辐射相当的Qmax[Ag Kα1 λ = 0.5594 Å，Qmax（2θ = 160°）=22.12 Å-1]。然而，对于弱散射材料，银靶束流能量较低，不足以收集高质量高角度散射数据，此时可以考虑使用钼靶实现[Mo Kα1 λ=0.7093 Å，Qmax（2θ =160°）=17.45 Å-1]。此外X射线全散射数据采集受到X射线固有属性的限制，即散射功率取决于样品的电子密度，原子形状因子f与原子序数Z成比例。因此难以从含有较多轻元素的样品或微孔样品获得高质量的PDF，且难以从同时包含轻重元素的X射线PDF中辨别轻元素的结构信息
如前所述，X射线对于轻元素分辨能力有限，而中子探针正是解决这一问题的有力工具。中子与原子核发生相互作用并进行散射，中子散射强度取决于元素的中子散射长度b，它在元素周期表中和原子同位素之间以一种看似随机的方式变化。因此，中子对于区分周期表中彼此相邻的原子或分析含有轻元素（如锂）的结构十分有用，我们可以利用非常不同的对比度特性从同时含有轻重元素的化合物中获得更多轻元素信息。
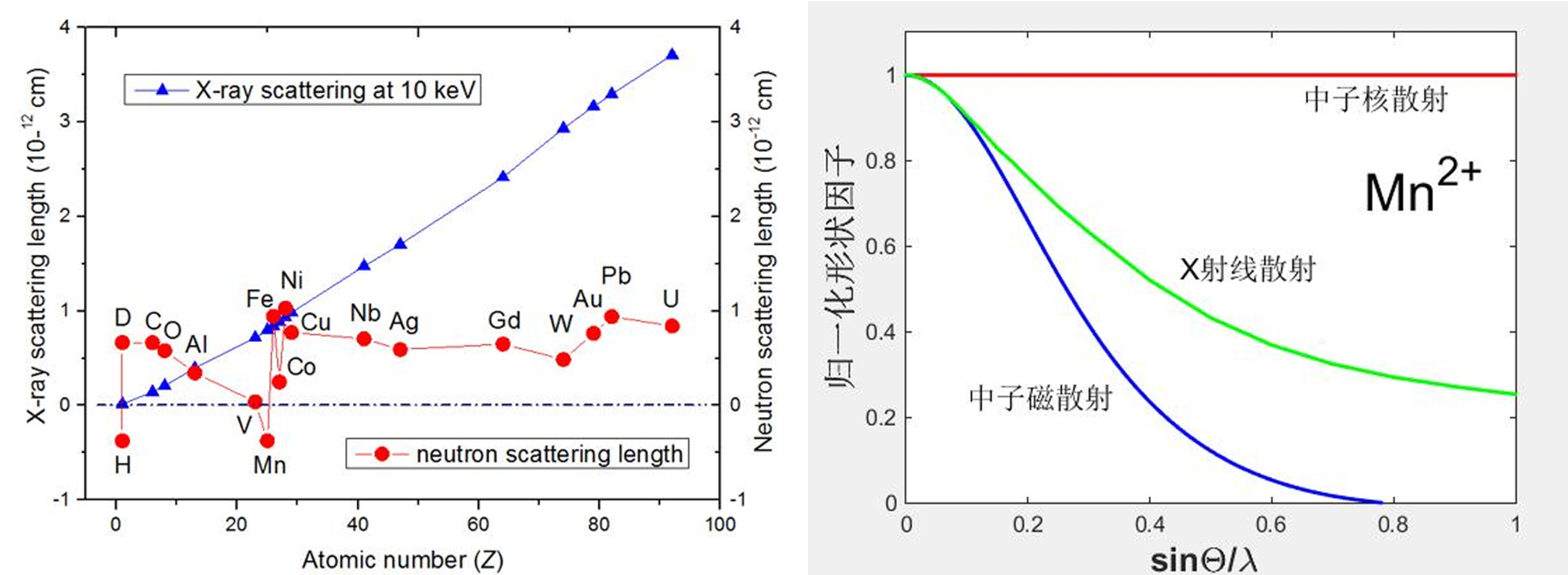
图 8 不同原子的X射线与中子散射长度（左）以及形状因子随sin(θ)/λ的变化（右）
同时由于中子也与电子的磁矩存在相互作用，因此通过中子全散射获得关于材料中磁性结构的信息也顺理成章。中子全散射的另一个优势在于中子散射长度b不随Q的变化而衰减。与X射线全散射数据相比，这提高了高Q范围的信噪比。中子全散射相较于X射线具有突出优势，但我们仍需认识到即使是最先进的散裂中子源，其中子通量也远低于同步辐射X射线通量，这代表中子全散射数据采集需要花费更长的时间以及更大量的样品，同时测试样品需要考虑到某些特定的同位素，例如氢，容易对中子产生大量的非相干散射，进而影响数据信噪比。考虑到中子散射资源的宝贵性，强烈建议在进行中子散射测试之前与线站谱仪科学家进行充分沟通。
图 9 我国部分具备开展PDF实验条件的同步辐射光源和中子源
X射线全散射测试样品多装载于玻璃及Kapton毛细管之中，这主要是考虑到易于密封和运输，且便于在线站测试端中快速换样。毛细管可以适配粉末、悬浮液、液体、凝胶等多种样品形态。在无法制备粉末样品的情况下，也可以通过将片状、块状样品通过Kapton胶带固定于测试金属窗口中心并保持与入射束的垂直。中子全散射测试样品则装载于线站合金样品管中便于快速换样装置夹取。正式测试时，同步辐射线站多通过大型面探测器采集散射数据，这样可以在单次测量中覆盖较宽的2θ角度范围，而飞行时间中子则通过环形分布的探测器采集中子数据。
全散射是一种弹性相干散射过程，而当X射线/中子束与样品相互作用时，还将发生非弹性、非相干的一系列相互作用，此外还存在样品对光束的吸收、荧光，以及多重散射等。此外，测量的数据还可能包含来自线束路径中的空气的信号以及测量仪器本身的干扰。因此，我们同样需要测试空样品管及标准样品（Si或Ni）的数据，用于对数据进行校正，以便我们从中分离出弹性相干散射信号。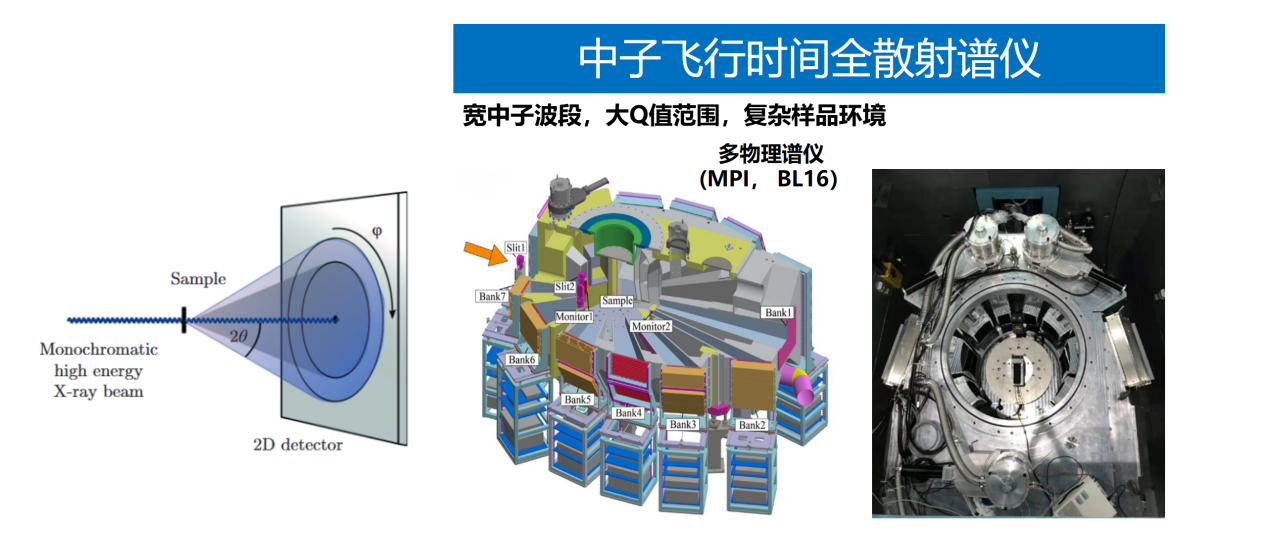 
图 10 同步辐射面探测器示意图（左）与飞行时间中子全散射谱仪（右）
在完成高质量全散射数据测量后，需要对数据进行转化并得到校正规约后的PDF函数，之后的数据分析过程将基于PDF函数来完成。通过对背景强度和Q值范围等参数的调整，从背景全散射数据和样品的全散射数据中转换得到对应的PDF函数。
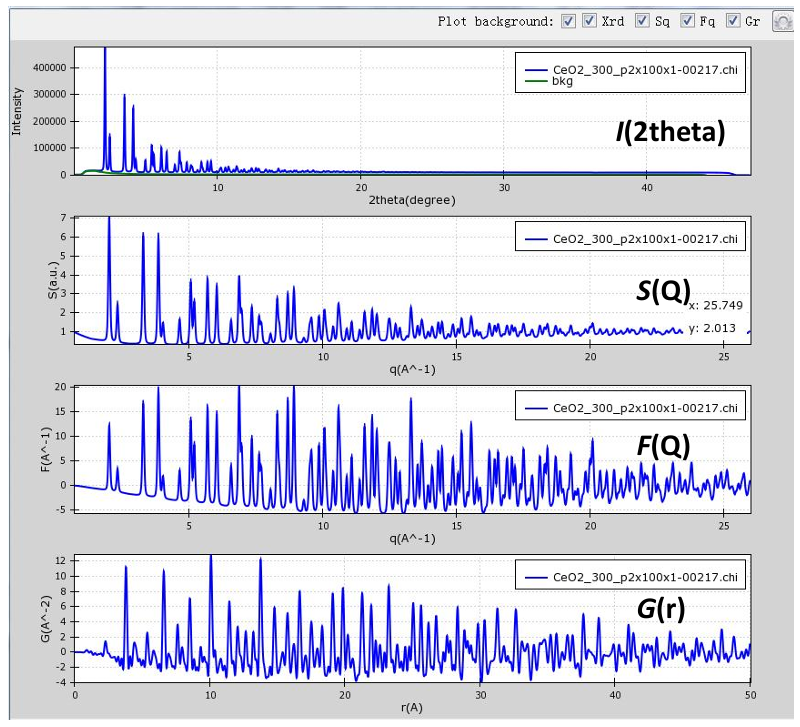
图 11 从全散射数据到PDF函数的规约转化过程
数据分析的第一步从校正规约后的PDF函数出发。如前所述，PDF函数本身包含了丰富的直观信息，甚至无需任何建模就可以从峰位和峰宽进行直观的推断。而通过建立原子结构模型并调参拟合PDF图谱能得到更为详细的结构信息，这一方法与晶体衍射的Rietveld方法完全类似。但相较于衍射拟合所构建的平均原子结构模型，PDF拟合所需构建的模型需要考虑到原子的无序排布或位点偏移。因此，最常见的是考虑将所有原子放入一个“盒子”中，通过在“盒子”中调整各个原子的位置及“盒子”大小或形状实现对PDF图谱的拟合。如果被研究材料结构相对均一有序，那么这个“盒子”可以直接等同于晶体学中的单胞，能符合一定的对称性规则，这类建模方法称为“小盒子”模型。但在更复杂的情况下，我们需要更大的“盒子”以描述局部结构中被破坏的对称性，这类似一种“超级晶胞”，其中甚至可以包含数千个原子，这类建模方法可以称之为“大盒子”模型，而这种建模的分析基础常依托于逆向蒙特卡罗方法。常用的PDF函数拟合分析工具多种多样，这里简单介绍PDFgui和TOPAS的使用。
5.1 PDFgui应用：PDFgui是一种使用广泛的PDF函数分析工具，它是完全开源免费的。该软件基于“小盒子”模型对于X射线/中子PDF图谱进行拟合，其工作流程是通过导入PDF数据以及初始晶胞结构来为我们待拟合数据的结构设置一个模型。拟合过程即通过调整最小二乘法精修模型中的可变参数，直到实验和计算的PDF图谱之间获得良好的一致性。PDFgui的应用窗口如图12所示，它支持基于CIF（晶体学信息文件）的晶体结构模型导入或手动添加原子，同时能够实现从初始晶体结构模型出发的模拟PDF图谱计算以及图谱拟合。
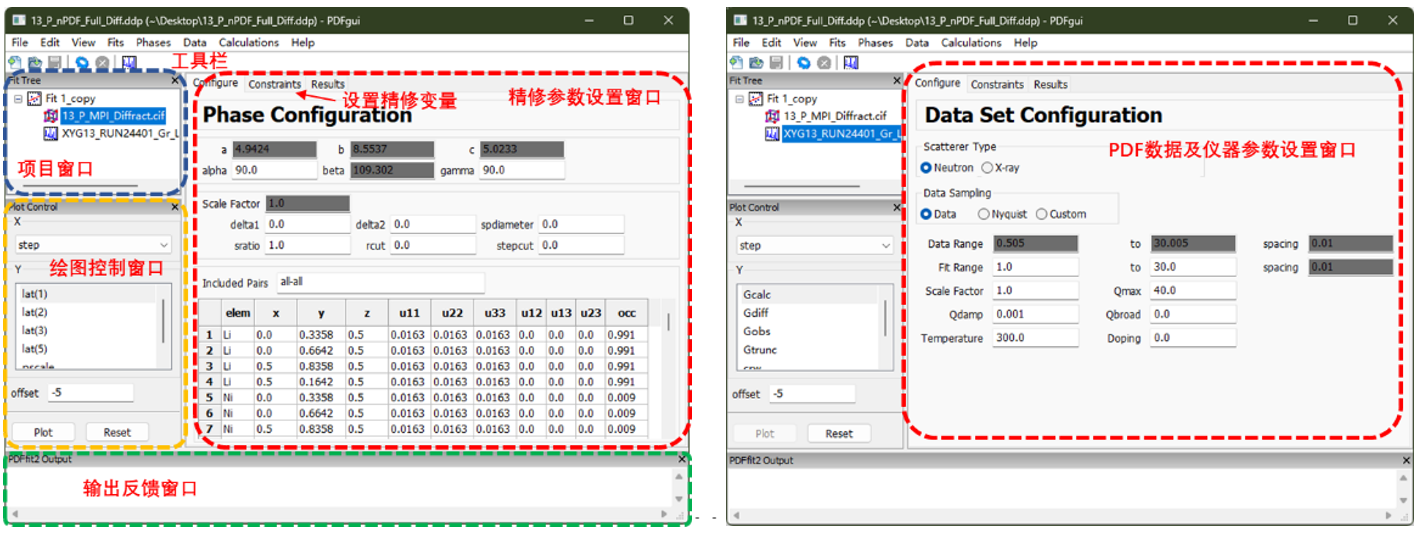图12 PDFgui软件操作界面
详细的软件使用方法可以查阅PDFgui软件使用手册，在此处我们主要介绍相关拟合参数。与Rietveld精修类似，PDFgui软件的精修参数同样包含比例因子、结构参数、仪器参数、相关原子运动修正参数、结构相干性参数等。其中比例因子控制PDF的整体强度，结构参数包含晶胞参数（a、b、c、α、β、γ），以及原子分数坐标（x、y、z）和原子位移因子（U11、U22、U33等）。仪器参数包含Qdamp（阻尼参数）和Qbroad（仪器分辨率校正参数），前者描述因仪器分辨率或样品尺寸效应造成的PDF强度随r的衰减程度，后者描述因仪器探测能力等原因造成的实空间峰形宽化。这两个参数正是通过对标准样品（Si或Ni等）的全谱拟合获得，且在针对样品的拟合时保持固定即可。相关原子运动修正参数包括δ1、δ2与sratio。对于近邻原子来说，它们的热振动存在关联，这使得PDF图谱低r值范围的峰变得尖锐因此需要通过相关原子运动修正参数进行描述。但需要注意的是“δ1”和“δ2”参数之间的差异非常小，这意味着如果同时精修，它们将强关联。因此在进行拟合时，应该选择其一使用，并将另一个设置为零。最后是结构相干性参数spdiameter，它用于描述球形颗粒尺寸大小。在纳米材料的全散射实验中，由于纳米颗粒的有限尺寸会引入较强的样品阻尼，因此可以通过在全谱精修的过程中引入spdiameter参数，它假设了球形颗粒的尺寸从而得到相关的样品阻尼。
当我们完成对参数的精修步骤后，我们可以在绘图窗口直观的看到精修图谱的拟合程度与差值曲线。同时结合尽可能低的Rw值，并确保所有精修的参数与结构模型具备合理的物理意义。
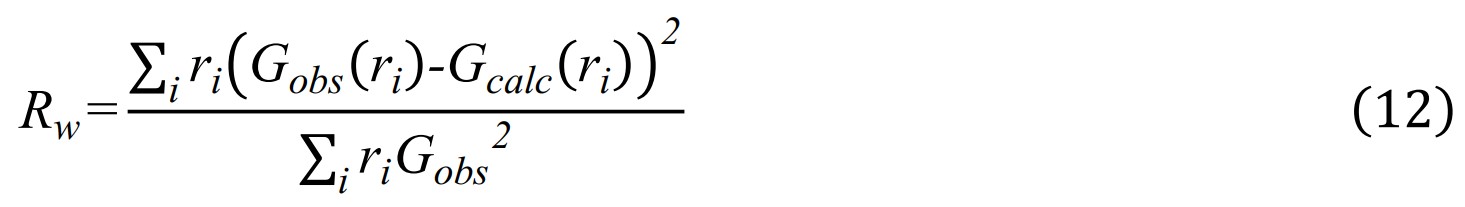
5.2 TOPAS应用: TOPAS是一款在材料科学领域广泛应用的高级粉末衍射分析软件，其核心优势在于它灵活的宏语言，该语言能支持用户以完全通用的方式定义方程，为用户提供了极高的灵活性和精确控制能力，尤其擅长处理复杂体系。该软件不仅能够进行常规的Rietveld精修，还深度集成了对原子对分布函数分析的支持。在PDF分析方面，在基于初始结构模型（如晶胞参数a、b、c、α、β、γ、原子坐标x、y、z）的基础上，用户还可以选择多种峰型函数（本质上来源于原子的热振动及无序度或键长畸变导致的实空间峰的展宽），如beq_r_min、beq_spherical、beq_rlo_spherical、beq_rcut_spherical、beq_rcut_rlo_spherical以及beq_empirical等6种热振动函数可选，此外在PDFgui所采用的beq_PDFfit2函数也在TOPAS中得到了引入，这些函数通过不同数学形式描述beq的空间分布，用户需根据材料特性（如无序类型、对称性）选择最合适的模型。beq_PDFfit2在两个软件中均被采用，其核心优势在于将原子热振动、局域结构畸变和仪器效应整合到一个物理模型中。相比传统分段beq函数，它通过Uiso（各向同性位移）、rcut（短程有序截断）、δ1/δ2（非谐振动校正）和 qbroad（关联仪器分辨率）等参数，直接关联 PDF实验数据的实空间峰形特征，既能精确描述近程有序区的非谐效应（如低r区峰形不对称），又可优化长程无序的展宽行为，显著提升纳米材料、强关联体系等复杂结构的拟合精度，同时减少参数冗余，避免传统模型的过度简化假设。用户可以通过编写结构化的文本输入文件（inp文件）来定义分析任务。该文件包含：实验数据路径、结构模型（晶胞、原子坐标、温度因子等）和其余参数等。TOPAS官方教程和用户社区常推荐 jEdit 作为首选编辑器，它支持直接运行模拟并查看日志，jEdit和TOPAS的用户界面如图13所示。
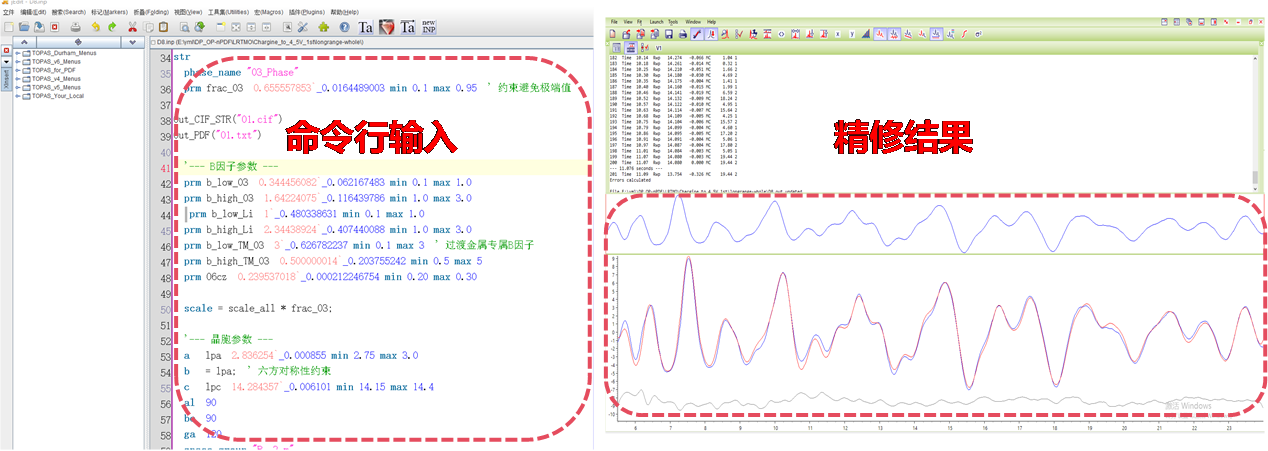
图 13 jEdit和TOPAS软件操作界面
同样，当完成对参数的精修步骤后，可以在绘图窗口直观的看到精修图谱的拟合程度与差值曲线。同时结合尽可能低的Rw值，确保所有精修的参数与结构模型具备合理的物理意义。
6. 材料局域结构的对分布函数分析应用实例
随着现代材料逐步向精细结构调控方向发展，传统晶体学手段往往难以有效揭示局部无序或结构畸变、纳米结构与效应和界面或非晶结构等关键信息。对分布函数（PDF）技术，因其具有揭示原子尺度的局域结构和无序特征的能力，正逐渐成为研究材料构-效关系的重要工具，在能源、功能材料等领域受到广泛应用。
对于储能材料 (如氧化物正极材料、固态电解质、石墨类负极材料) 的深入研究表明，材料性能的提升依赖于对其原子尺度结构的精准解析。材料在充放电过程中局部结构畸变、缺陷演化和离子无序化将直接影响电池体系能量密度与循环寿命。通过传统的结构表征手段如X射线衍射 (XRD) 等难以探测此类局域结构信息，同时对于石墨负极等非晶态材料的短程有序信息也难以获取。PDF分析可提供原子尺度的局域结构信息，揭示材料短程有序/无序特征。如图14所示，我们采用中子对分布函数 (nPDF) 分析方法对富锰层状氧化物 (MRLOs) 中阳离子长程/短程有序结构开展研究[10]。结合对称性分析，该研究在常见的MRLO中发现了新型的阳离子有序结构。通过调节氧空位的形成，材料从短程到长程范围内阳离子的有序转变被破坏。这一短程无序结构有效地减轻了协同Jahn-Teller畸变，实现材料在循环过程中的结构稳定性。
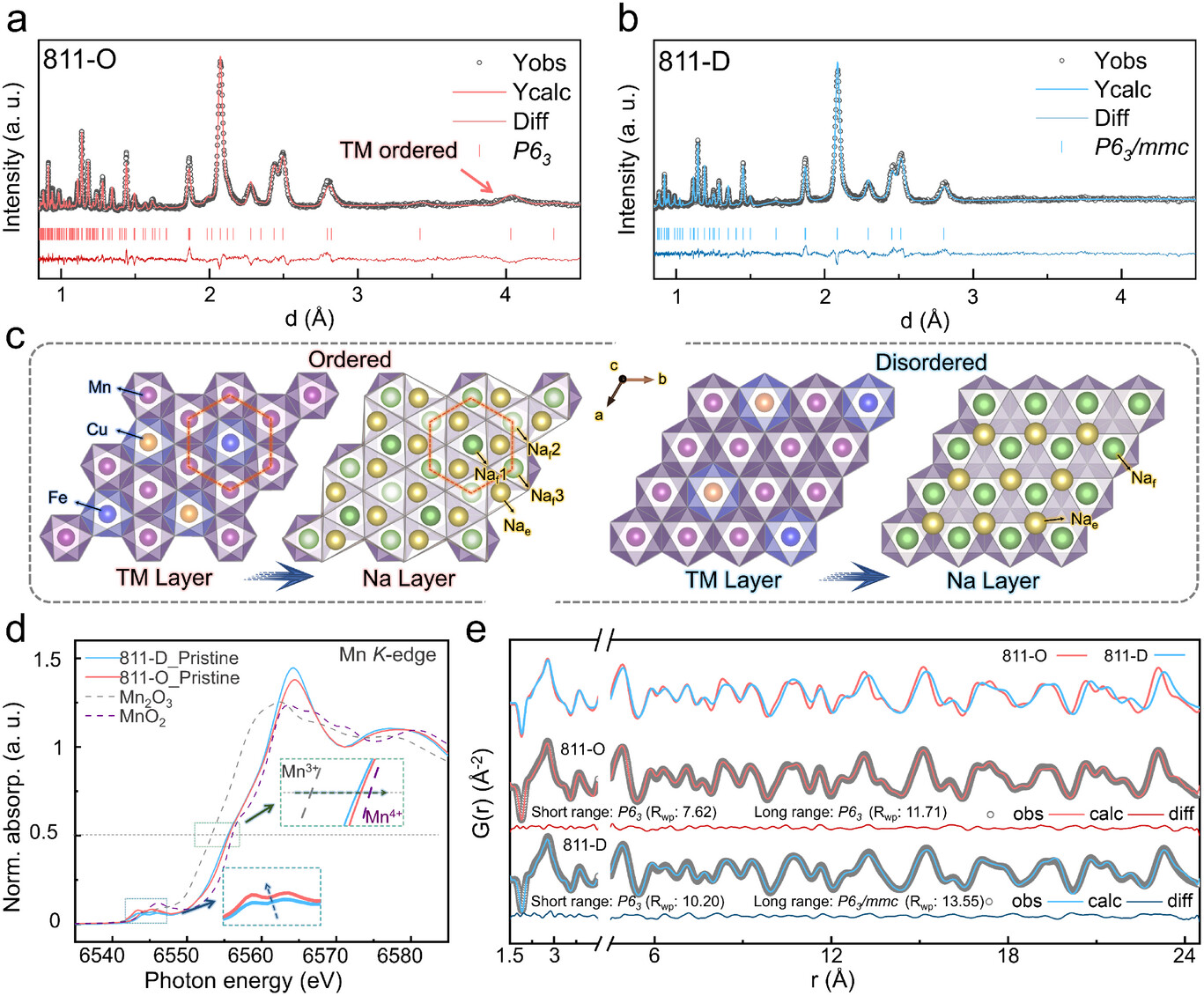
图 14 合成样品的初始长程和短程结构示意，811-O (a) 和811-D (b) 的Rietveld NPD细化结果；(c) 沿[001]区轴具有TM有序和无序排列的晶体结构示意图；(d) 811-O、811-D和相应标准氧化物样品的归一化Mn K边XANES光谱； (e), (f) 具有不同长程/短程对称性样品的nPDF拟合结果。
中子全散射及对应的PDF方法相较于其他束流源所具有的另一个优势便是中子对于轻元素的高敏感性。因此通过nPDF分析能得到轻元素原子对键长的重要信息。例如我们通过nPDF探究了Ru掺杂的Na0.67Fe0.5Mn0.5O2材料中可能存在的阴离子氧化还原活性[11]。其中nPDF图谱（图15）直观显示，代表性样品FMR-0在2.83 Å处对应于层内O-O键的峰相对于FMR-0.05样品偏左 (~2.86Å) ，表明FMR-0具有更短的层内O-O键。同时在2.5–2.6Å处FMR-0.05显示增强的峰形。上述发现可以被认为是形成具有较短键的O-O对的实验证据，与氧阴离子的氧化有关。
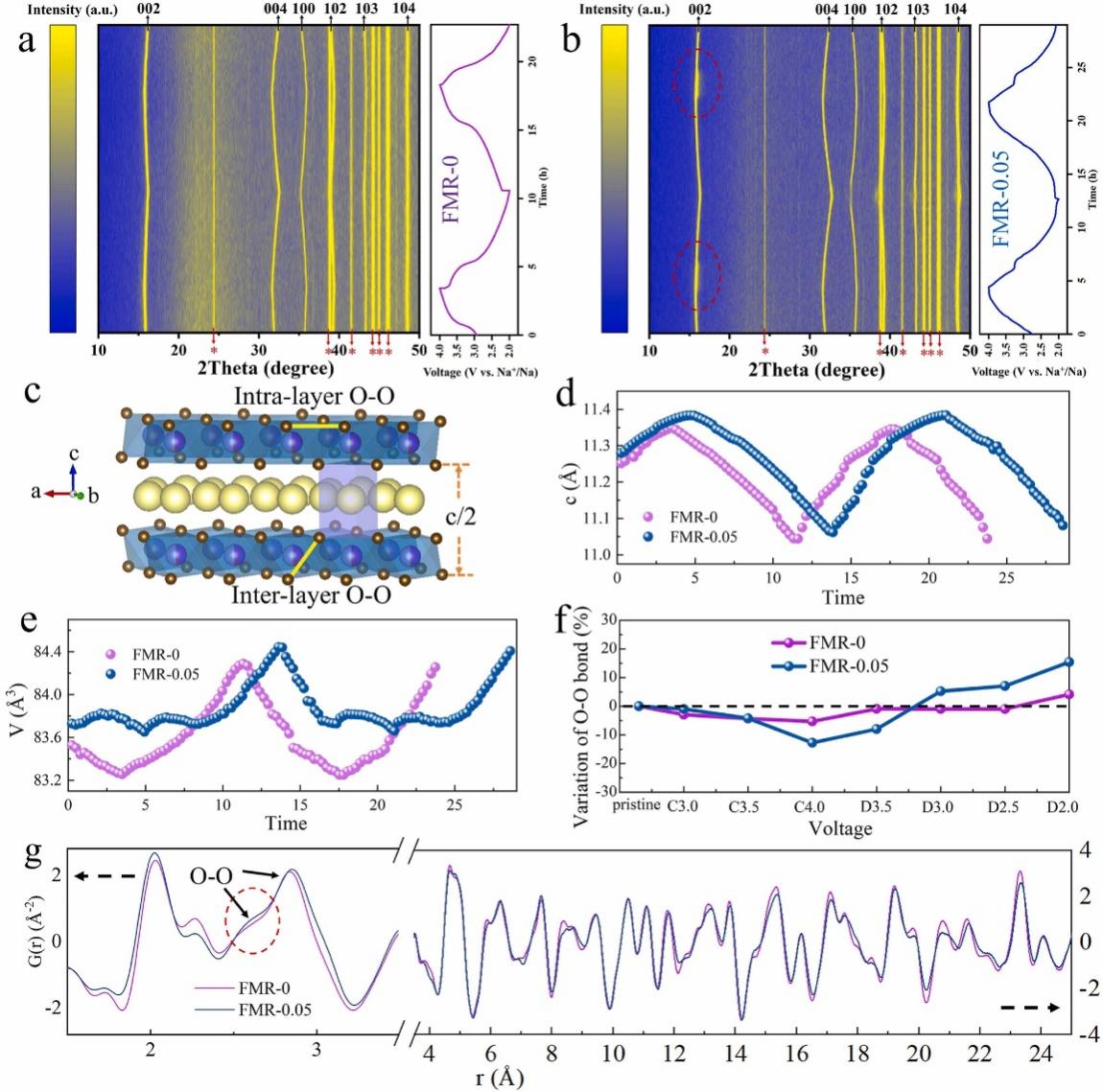
图 15 (a，b) FMR-0和FMR-0.05在10–50°的2θ范围内的原位XRD图谱；(c) FMR-x的相应晶体结构；(d，e) 放电/充电过程中FMR-0和FMR-0.05晶格参数的变化；(f) 在不同电压状态下层间O-O键长的相应变化；(g) 在充电状态 (4.0 V) 下收集的FMR-0和FMR-0.05的中子PDF图谱。
在无序岩盐相材料 (DRX) 的研究中阳离子的短程有序结构 (SRO) 会极大影响DRX正极材料的电化学性能，如图16所示，Sun等人[12]结合中子全散射和逆蒙特卡洛方法还原了其微-介观原子排列特征，证实并拓展了无序岩盐结构中与SRO相关的锂离子传导渗流理论。
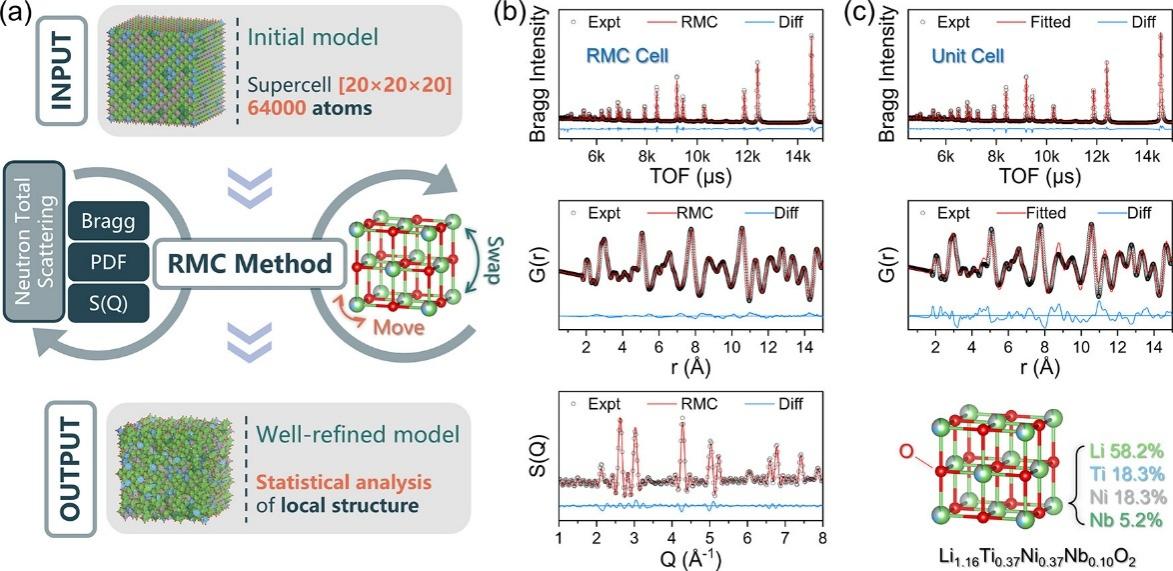
图 16 (a) RMC建模和拟合工作流程示意图；(b) Bragg、G(r) 和 S(Q) 数据的RMC拟合结果；（c）布拉格和 G(r) 数据的晶胞拟合结果;单位晶胞显示在插图中，并注释了位点占有和化学计量比。
在非晶石墨负极材料的研究中，McNutt等[13]借助中子全散射对于碳材料在锂离子插层过程中局域结构的演变规律进行探究。该团队发现锂离子并非直接嵌入碳层之间，而是会优先存储于结晶碳和非晶碳的界面处，并与氢原子结合，其界面处的储锂量与边界的比表面积正成比，这对于碳负极材料的嵌锂机制提出了全新见解。
功能材料（如超导材料、铁电材料等）的性能常源于电子/声子与局部结构的耦合，而这类材料中的纳米相畴、局域畸变等非均匀性结构难以通过平均结构表征手段分析。因此，通过PDF分析能有效捕捉短程（< 5 nm）与中程（5-20 nm）结构信息，量化局域畸变，从而关联局域结构变化与热电系数、介电常数等宏观物理参数。例如Bozin等人[14]通过中子PDF研究了典型高温超导体系La2-xBaxCuO4（0≤x≤0.3）中局部CuO6八面体的构型变化（如图17）。由于能带结构对Cu-O键几何形状的强烈响应，CuO6八面体的构型变化极大地影响铜酸盐的超导电性。因此通过PDF分析不同非化学计量组成下的CuO6八面体的局部构型能够有效建立该体系的掺杂效应和超导电性间的关联。
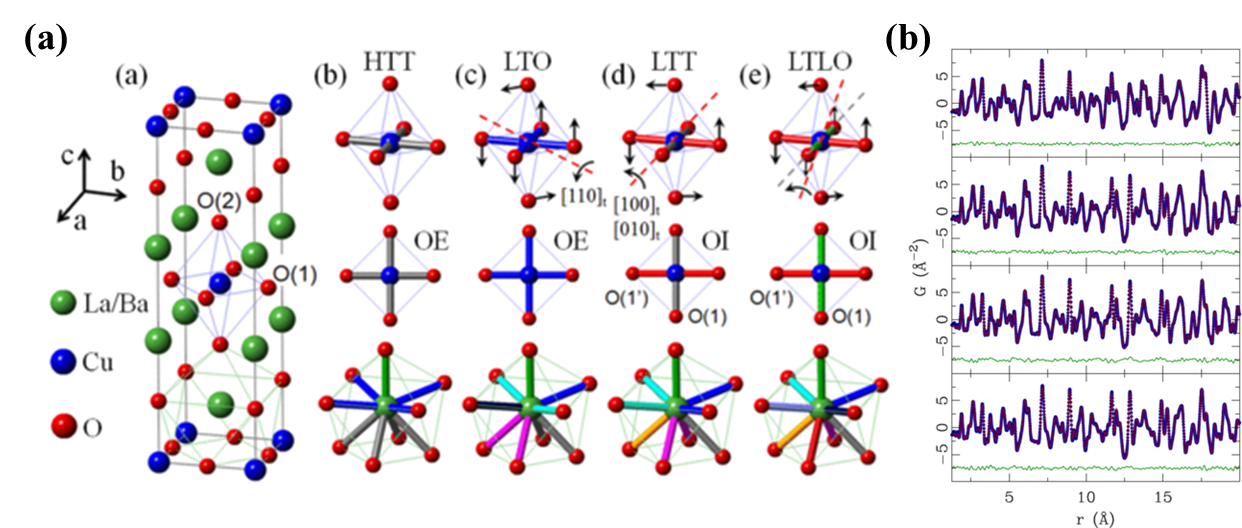
图 17 La2-xBaxCuO4在高温四方相I4/mmm (HTT)、低温正交相Bmab (LTO)、低温四方 相P42/ncm (LTT) 和低温过渡正交相Pccn (LTLO)中的结构细节；及 (b)对应的PDF数据拟合结构
如图18所示，对于压电材料中准同型相界（MPB）的研究，PDF方法常用于探测压电MPB附近的结构。例如，作为一种典型的压电材料，PbZr1-xTixO3（PZT）通常被认为在MPB上显示出四方到菱方结构的相转变。然而，这种相变被对称性所限制，而常被认为由单斜相介导。为了阐明这种中间单斜相结构，进行了中子PDF与RMC建模相结合的研究，以研究MPB的短程和长程结构。[15]
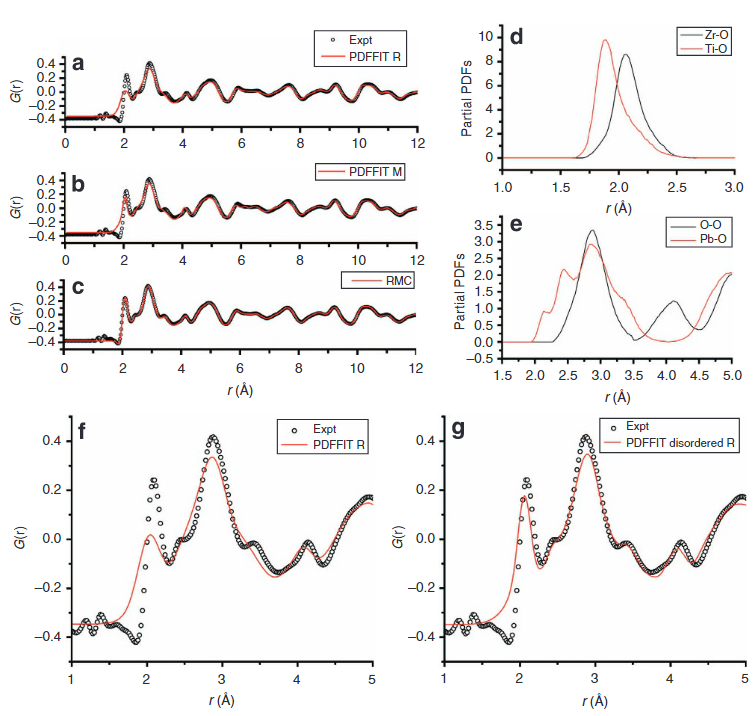
图 18 (a-c) 分别使用菱方相、单斜相结构和逆蒙特卡洛方法对PDF拟合的结果；(d) Zr-O和Ti-O原子对的短程区域PDF峰；(e) 来自RMC模型的Pb-O和O-O原子对的短程区域PDF峰；(f) 图a的放大视图，显示了原始数据和拟合结果之间的差异；(g) 添加围绕[111]轴的无序 Pb位移后拟合结果放大视图。
作为纳米材料主要研究方向之一的量子点 (QD) 同样适合通过 PDF方法开展研究。由于纳米级QD晶格仅具有短程有序结构，PDF技术可以探测材料不均匀的键合环境、相偏析与结构缺陷等。例如Beecher等人[16]通过PDF分析研究了CdSe团簇的结构不均匀性。结果表明，团簇的核心是由{111}端接的金字塔形纳米结构和闪锌矿原子堆积而成。Petkov等人[17]利用PDF方法研究PbSe纳米晶体中的局部无序与颗粒尺寸的关联行为（如图19）。该研究通过用各种有限尺寸模型拟合对分布函数G(r)，其中缺硒模型得到最高的拟合优度，表明纳米级PbSe的局部结构存在畸变，同时元素组成偏离化学计量。
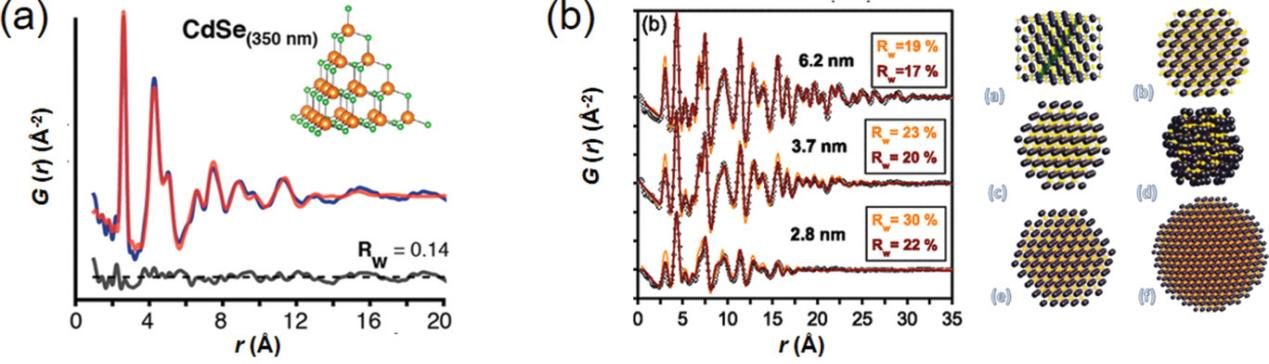
图 19 (a) CdSe量子点的PDF拟合图像。插图为拟合采用的闪锌矿金字塔结构模型；(b) 基于完全化学计量 (橙色线) 和非化学计量模型 (红色线) 的PbSe量子点的PDF拟合图像，并给出了具有不同表面构型的结构模型。
7. 总结
PDF技术能够突破传统衍射的周期性限制，在实空间直接解析原子尺度的局域结构特征，包括如键长、配位数、无序度及纳米尺寸效应。该技术兼容中子和X射线甚至电子探针。其中，中子PDF凭借其对轻元素和磁结构的敏感性，成为解析能源材料及磁性材料体系的关键工具，X射线PDF依托高能同步辐射实现高通量的快速测量，电子PDF则助力纳米材料微区局域结构分析。在应用层面，PDF技术已深入能源材料（如揭示正极材料局域畸变、锂离子输运机制）、功能材料（如关联高温超导体局域构型、铁电体极化微观机制）及非晶/纳米体系的结构解析，成为连接原子微观局域结构与宏观性能的核心表征手段之一。未来PDF技术发展趋势将聚焦于高通量实验与智能算法融合、多尺度技术联用和原位工况表征，进一步推动PDF方法在新型材料设计与优化中的革新性应用。
参考文献
[1] 李强, 林鲲, 邢献然. 基于全散射技术局域结构确定与凝聚态物质[J]. 化学进展, 2020, 32(08): 1219-1230.
[2] H. Zhu, Y. Huang, J. Ren, B. Zhang, Y. Ke, A. K. ‐Y. Jen, Q. Zhang, X. Wang, Q. Liu, Adv. Sci. 2021, 8, 2003534.
[3] M. W. Terban, S. J. L. Billinge, Chem. Rev. 2022, 122, 1208.
[4] T. Kakeshita, T. Fukuda, A. Saxena, A. Planes, Eds., Disorder and Strain-Induced Complexity in Functional Materials, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012.
[5] N. Dragoe, D. Bérardan, Science 2019, 366, 573.
[6] B. Sacépé, T. Dubouchet, C. Chapelier, M. Sanquer, M. Ovadia, D. Shahar, M. Feigel’man, L. Ioffe, Nat. Phys. 2011, 7, 239.
[7] H. M. Rietveld, J. Appl. Crystallogr. 1969, 2, 65.
[8] S. J. L. Billinge, Atomic Pair Distribution Function Analysis: A Primer, Oxford University Press, Incorporated, Oxford, 2024.
[9] P. F. Peterson, D. Olds, M. T. McDonnell, K. Page, J. Appl. Crystallogr. 2021, 54, 317.
[10] M. Yang, T. Yang, M. Dong, Z. Huang, Y. Pu, L. Jin, R. Wang, Y. Luo, T. Zeng, Y. Tang, J. Chen, R. E. Dunin-Borkowski, Z. Chen, Y. Qiao, Y. Xiao, Adv. Mater. n.d., n/a, 2500984.
[11] Chen Z., Yang M., Chen G., Tang G., Huang Z., Chu M., Qi R., Li S., Wang R., Wang C., Zhang T., Zhai J., Zhao W., Zhang J., Chen J., He L., Xu J., Yin W., Wang J., Xiao Y., Nano Energy 2022, 94, 106958.
[12] Y. Sun, S. Jiao, J. Wang, Y. Zhang, J. Liu, X. Wang, L. Kang, X. Yu, H. Li, L. Chen, X. Huang, J. Am. Chem. Soc. 2023, jacs.3c02041.
[13] N. W. McNutt, O. Rios, V. Maroulas, D. J. Keffer, Carbon 2017, 111, 828.
[14] E. S. Bozin, R. Zhong, K. R. Knox, G. Gu, J. P. Hill, J. M. Tranquada, S. J. L. Billinge, Phys. Rev. B 2015, 91, 054521.
[15] N. Zhang, H. Yokota, A. M. Glazer, Z. Ren, D. A. Keen, D. S. Keeble, P. A. Thomas, Z.-G. Ye, Nat. Commun. 2014, 5, 5231.
[16] A. N. Beecher, X. Yang, J. H. Palmer, A. L. LaGrassa, P. Juhas, S. J. L. Billinge, J. S. Owen, J. Am. Chem. Soc. 2014, 136, 10645.
[17] V. Petkov, S. D. Shastri, Phys. Rev. B 2010, 81, 165428.